A uniform rod of length 2a is held at inclination α with the horizontla with its lower end at a height h above a horizontal plane surface and is let fall. It rebounds elastically from the plane. If you just before the other end touches the plane the rod makes the same angle with the horizontal, find the value of h in terms of a and α.
The correct Answer is:h=⎛⎝aα(1+3cos2α)212cosα(1−3cos2α)⎞⎠
Topper's Solved these Questions
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABook:NN GHOSHChapter:ROTATIONAL DYNAMICS, MOMENT OF INERTIAExercise:Exercises
Explore 42 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBook:NN GHOSHChapter:MOMENT, TORQUE, EQUILIBRIUM OF BODIESExercise:Exercises
Explore 33 Videos
- SATURATED AND UNSATURATED VAPOURBook:NN GHOSHChapter:SATURATED AND UNSATURATED VAPOURExercise:All Questions
Explore 1 Video
Similar Questions
A uniform rod of length 2l is placed with one end in contact with the horizontal table and is then inclined at an angle α to the horizontal and allowed to fall. When it becomes horizontal, its angular velocity will be
View SolutionA uniform rod of length 2L is placed with one end in contact with the horizontal and is then inclined at an angle a to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
View Solution
Knowledge Check
A uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
Aits center of mass moves vertically downwards on a straight lineBIts center of mass remains in restCthe rod rotates about a vertical axisDBoth a and c are correctA uniform rod of length 2l is placed with one end in contact with the horizontal table and is then inclined at an angle α to the horizontal and allowed to fall. When it becomes horizontal, its angular velocity will be
Aω=√(3gsinα2l)Bω=√(2l3gsinα)Cω=√(gsinαl)Dω=√(lgsinα)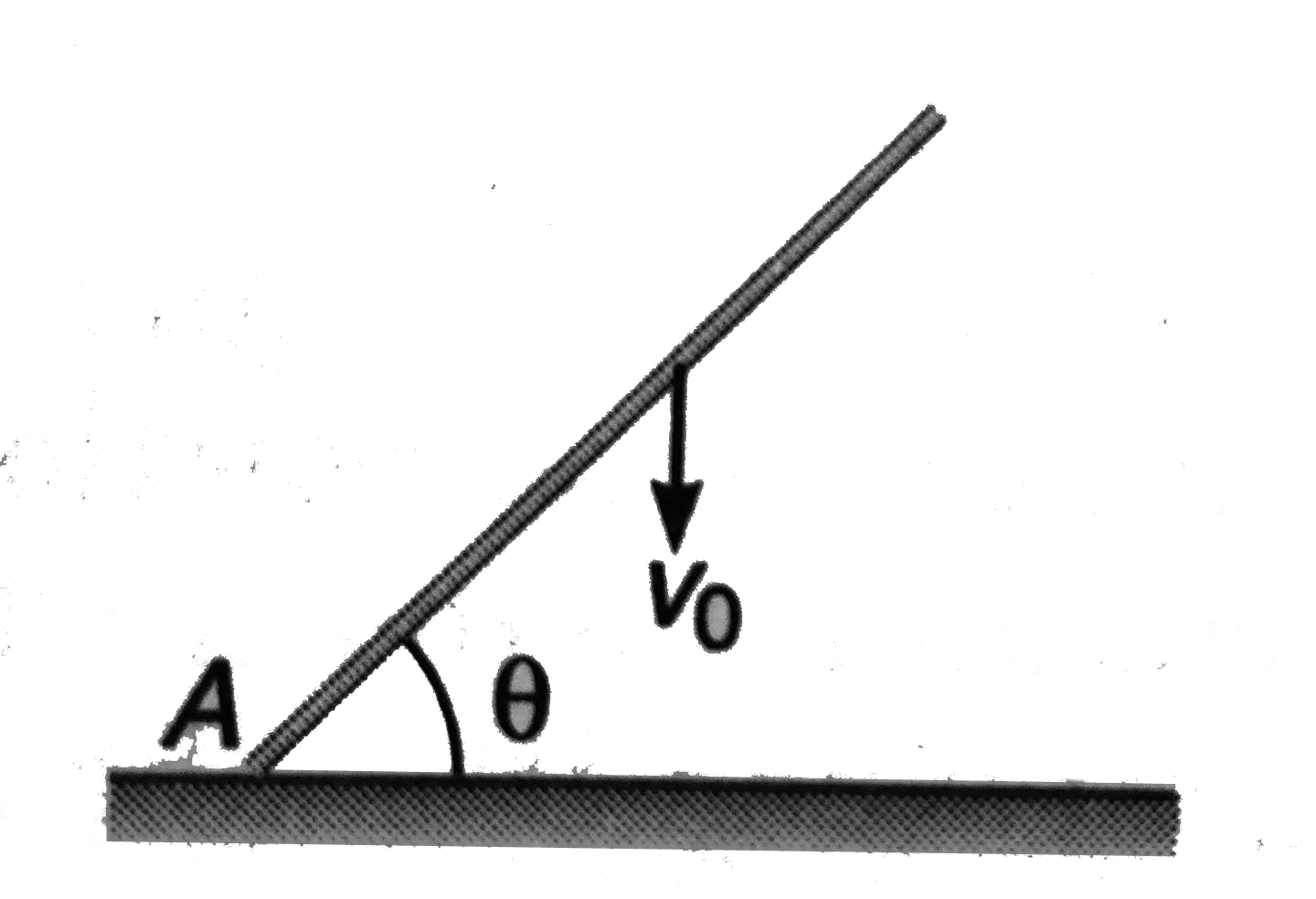
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.A3vcosθ2lB12vcosθl(1+cos2)θC12vcosθl(1+3cos2θ)Dvcosθl(1+cos2θ)
A uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform rod of length L is placed with one end in contact with the horizontal and is then inclined at an angle α to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
View SolutionA uniform rod of length l is placed with one end in contact with the horizontal and is then inclined at an angle a to the horizontal and allowed to fall, without slipping at contact point. When it becomes horizontal, its angular velocity will be
View Solution
