The forecasted monthly sales of always sunny sunscreen are presented in the figure above. For which period are the forecasted monthly sales figures strictly decreasing and then strictly increasing?
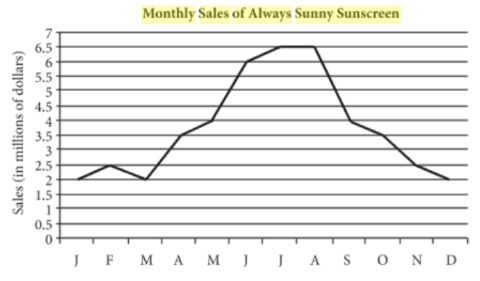
January to March
February to April
June to August
September to November
The correct Answer is:B
Topper's Solved these Questions
- FUN WITH FUNDAMENTALSBOOK - PRINCETONCHAPTER - FUN WITH FUNDAMENTALSEXERCISE - Fundamental Drill 1: No Calculator Section
4 Videos
- FUN WITH FUNDAMENTALSBOOK - PRINCETONCHAPTER - FUN WITH FUNDAMENTALSEXERCISE - Fundamental Drill 2: Calculator- Permitted Section
6 Videos
- FUN WITH FUNDAMENTALSBOOK - PRINCETONCHAPTER - FUN WITH FUNDAMENTALSEXERCISE - DRILL 5
4 Videos
- ARITHMETICBOOK - PRINCETONCHAPTER - ARITHMETICEXERCISE - QUICK QUIZ #11
3 Videos
- FUNCTIONS AND GRAPHSBOOK - PRINCETONCHAPTER - FUNCTIONS AND GRAPHSEXERCISE - Functions and Graphs Drill 2: Calculator -Permitted Section
6 Videos
Similar Questions
Knowledge Check

The forecasted monthly sales of Always Sunny Sunscreen are presented in the figure above. Which of the following best describes the range of monthly sales , in millions of dollars, throughout the year shown?A2.5B3.5C4.0D4.5
Find the intervals in which the function f given by f(x)=sinx+cosx, 0≤x ≤2π is strictly increasing or strictly decreasing.
View SolutionDetermine the intervals in which the following functions are strictly increasing or strictly decreasing :
f(x)=2x3−3x2−36x+7.
View SolutionFind the intervals in which the function f given by f(x)=2x2−3xis(a) strictly increasing (b) strictly decreasing
View SolutionFind the interval in which
f(x)=x3−3x2−9x+20 is strictly increasing or strictly decreasing.
View SolutionFind the intervals in which the function f(x)=sinx+cosx,x∈[0,2π] is
(i) strictly increasing, (ii) strictly decreasing.
View SolutionFind the interval in which
f(x)=x3−3x2−9x+20 is strictly increasing or strictly decreasing.
View SolutionFind the intervals in which the function f given by f(x)=sinx−cosx,0≤x≤2π is strictly increasing or strictly decreasing.
View Solution
