Which of the following represents the statement " the sum of the squares of x and y iis equal to the sqaure root of the difference x and "?
x2+y2=√x−y
x2−y2=√x+y
(x+y)2=√x−√y
√x+y=√x−y2
The correct Answer is:A
Step by step video, text & image solution for Which of the following represents the statement " the sum of the squares of x and y iis equal to the sqaure root of the difference x and "? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PRINCETONCHAPTER - FUN WITH FUNDAMENTALSEXERCISE - Fundamental Drill 2: Calculator- Permitted Section6videos
FUN WITH FUNDAMENTALS
- BOOK - PRINCETONCHAPTER - FUN WITH FUNDAMENTALSEXERCISE - Example6videos
FUN WITH FUNDAMENTALS
- BOOK - PRINCETONCHAPTER - ARITHMETICEXERCISE - QUICK QUIZ #113videos
ARITHMETIC
- BOOK - PRINCETONCHAPTER - FUNCTIONS AND GRAPHSEXERCISE - Functions and Graphs Drill 2: Calculator -Permitted Section6videos
FUNCTIONS AND GRAPHS
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following is equivalent to the sum of any 3 consecutive odd integers, x, y, and z, suh that x < y < z ?
A3zB3yC3xD3x+2
If the sum of the roots of x2+bx+1=0, is equal to the sum of their squares, then b =
View SolutionIF the sum of the square of the roots of x2+px−3=0 is 10 then the values of p=
View SolutionConsider the graph of y = f(x) as shown in the following figure.
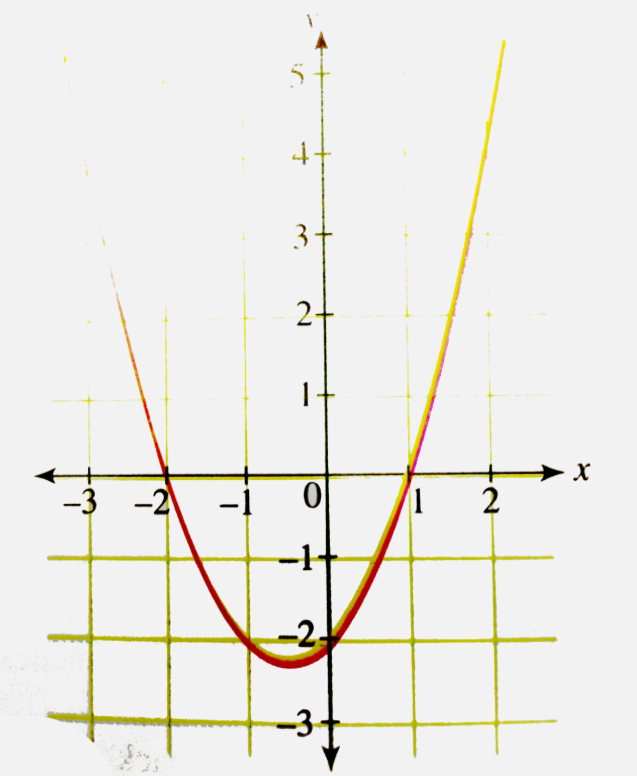
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .View SolutionFind the square of : (ii) 2x−5y
View SolutionThe number x is 2 more than the number y. If the sum of the squares of x and y is 34, find the product of x and y.
Given : x−y=2andx2+y2=34
To find the value of xy.View SolutionNegate the following statement: There exists a number which is equal to its square.
View SolutionFind a quadratic equation for which the sum of the roots is 7 and the sum of the squares of the roots is 25.
View Solution

