If n and s are integers, and , which of the following could be a value of n+s?
The correct Answer is:A
To solve the problem step by step, we will analyze the inequalities given and find the possible values of n+s.
Step 1: Analyze the first inequality
The first inequality given is:
n+5<7
To isolate n, we subtract 5 from both sides:
n<7−5
n<2
Step 2: Analyze the second inequality
The second inequality given is:
s−6<−4
To isolate s, we add 6 to both sides:
s<−4+6
s<2
Step 3: Combine the inequalities
Now we have:
1. n<2 (from Step 1)
2. s<2 (from Step 2)
We want to find the possible values of n+s.
Step 4: Determine the maximum value of n+s
Since both n and s are less than 2, we can express this as:
n+s<2+2
n+s<4
Step 5: Check the options
Now we need to check which of the provided options could be a value of n+s:
- Option A: 2
- Option B: 4
- Option C: (not provided in the question)
- Option D: 6
From our calculation, we know that n+s<4. Therefore:
- Option A (2) is valid because 2<4.
- Option B (4) is not valid because 4 is not less than 4.
- Option D (6) is also not valid because 6>4.
Thus, the only possible value for n+s from the options given is:
2
The first inequality given is:
n+5<7
n<7−5
n<2
The second inequality given is:
s−6<−4
s<−4+6
s<2
Now we have:
1. n<2 (from Step 1)
2. s<2 (from Step 2)
Since both n and s are less than 2, we can express this as:
n+s<2+2
n+s<4
Now we need to check which of the provided options could be a value of n+s:
- Option A: 2
- Option B: 4
- Option C: (not provided in the question)
- Option D: 6
- Option A (2) is valid because 2<4.
- Option B (4) is not valid because 4 is not less than 4.
- Option D (6) is also not valid because 6>4.
2
Topper's Solved these Questions
Similar Questions
Knowledge Check
If 5 times a number n is subtracted from 15, the result is negative, Which of the following gives the possible value(s) for n?
A0 onlyB3 onlyC10 onlyDAll n gt 3If f(x) = n , where n is an integer such that n≤x<n+1, the range of f(x) is
Athe set of all real numbersBthe set of all positive integersCthe set of all integersDthe set of all negative integers
If I, n are positive integers , 0<f<1 and if (7+4√3)n=I+f, then show that I is an odd integer
View SolutionConsider the series 2016.n+2015.(n−1)+2014.(n−2)+2013.(n−3)+, where Sn is the sum of first n terns of the series. Which of the following is/are true. (a) sn=n(n+1)(6049−n)6 (b) sn=n(n+1)(3025−n)3 (c) S20=422030 (d) S20=420700
View SolutionIf I, n are positive integers , 0<f<1 and if (7+4√3)n=I+f,
then show that (I+f)(1−f)=1
View SolutionWhat could be the product(s) for the following SN1 reaction?
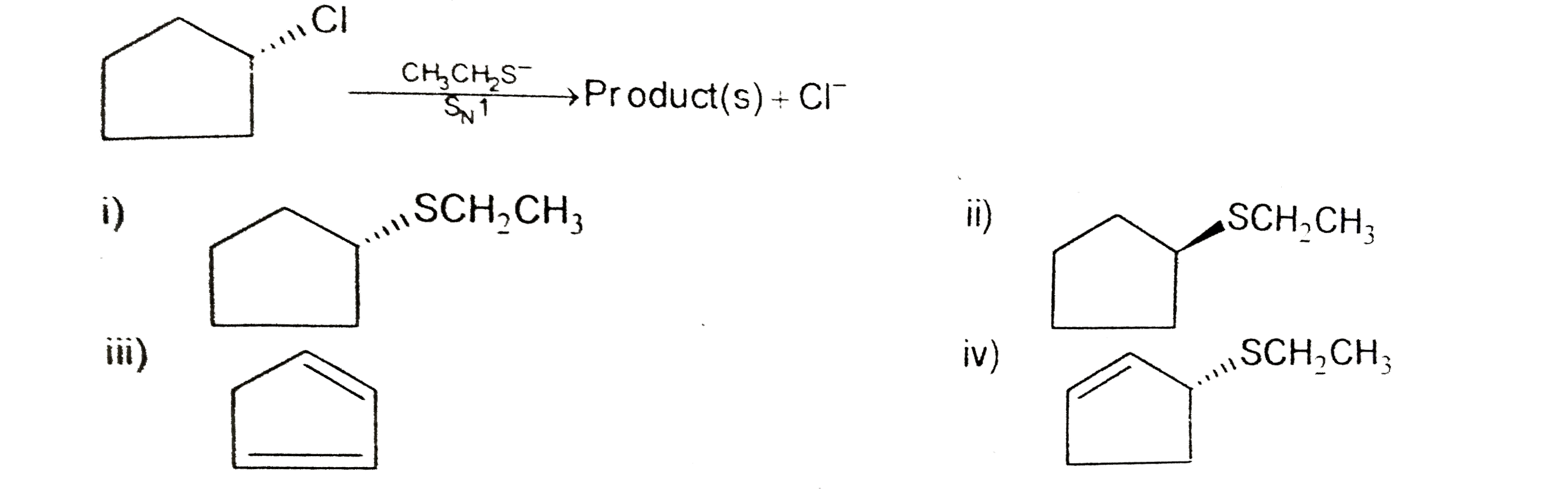
View SolutionSn=2n−5 for all integers n≥1. What is the 11th term of the sequence?
View SolutionIf (7+4√3)n+5+t , where n and s are
positive integers and t is a proper fraction , show that
(1 - t) (s + t) = 1
View Solution
