x2+y2−6x+8y=−9
The equation of the circle in xy-plane is shown above. What is the radius of the circle?
3
4
9
16
The correct Answer is:B
To find the radius of the circle given by the equation x2+y2−6x+8y=−9, we will follow these steps:
Step 1: Rewrite the equation in standard form
We start with the equation:
x2+y2−6x+8y=−9
To rewrite it in the standard form of a circle, we need to move −9 to the left side:
x2+y2−6x+8y+9=0
Step 2: Identify coefficients for the general circle equation
The general equation of a circle is given by:
x2+y2+2gx+2fy+c=0
From our rewritten equation, we can identify:
- The coefficient of x is −6, which means 2g=−6 so g=−3.
- The coefficient of y is 8, which means 2f=8 so f=4.
- The constant term c is 9.
Step 3: Calculate the radius
The radius r of the circle can be found using the formula:
r=√g2+f2−c
Substituting the values we found:
- g=−3
- f=4
- c=9
We calculate:
r=√(−3)2+(4)2−9
Calculating each term:
(−3)2=9and(4)2=16
So,
r=√9+16−9
This simplifies to:
r=√16=4
Conclusion
The radius of the circle is 4.
---
We start with the equation:
x2+y2−6x+8y=−9
To rewrite it in the standard form of a circle, we need to move −9 to the left side:
x2+y2−6x+8y+9=0
The general equation of a circle is given by:
x2+y2+2gx+2fy+c=0
From our rewritten equation, we can identify:
- The coefficient of x is −6, which means 2g=−6 so g=−3.
- The coefficient of y is 8, which means 2f=8 so f=4.
- The constant term c is 9.
The radius r of the circle can be found using the formula:
r=√g2+f2−c
Substituting the values we found:
- g=−3
- f=4
- c=9
r=√(−3)2+(4)2−9
Calculating each term:
(−3)2=9and(4)2=16
So,
r=√9+16−9
This simplifies to:
r=√16=4
The radius of the circle is 4.
Topper's Solved these Questions
Similar Questions
x2+6x+y2−8y=171
The equation of a circle in the xy-plane is shown above. What is the positive difference between the x-and y-coordinates of the center of the circle ?
View Solutionx2+20x+y2+16y=−20
The equation above defines a circle in the xy-plane. What are the coordinates of the centre of the circle ?
View Solution
Knowledge Check
x2+y2+4x−2y=−1
The equation of a circle in the xy-plane is shown above. What is the radius of the circle?A2B3C4D9x2+y2−6x+8y=56
What is the area of a circle whose equation is given above?A25πB81πC162πD6,561π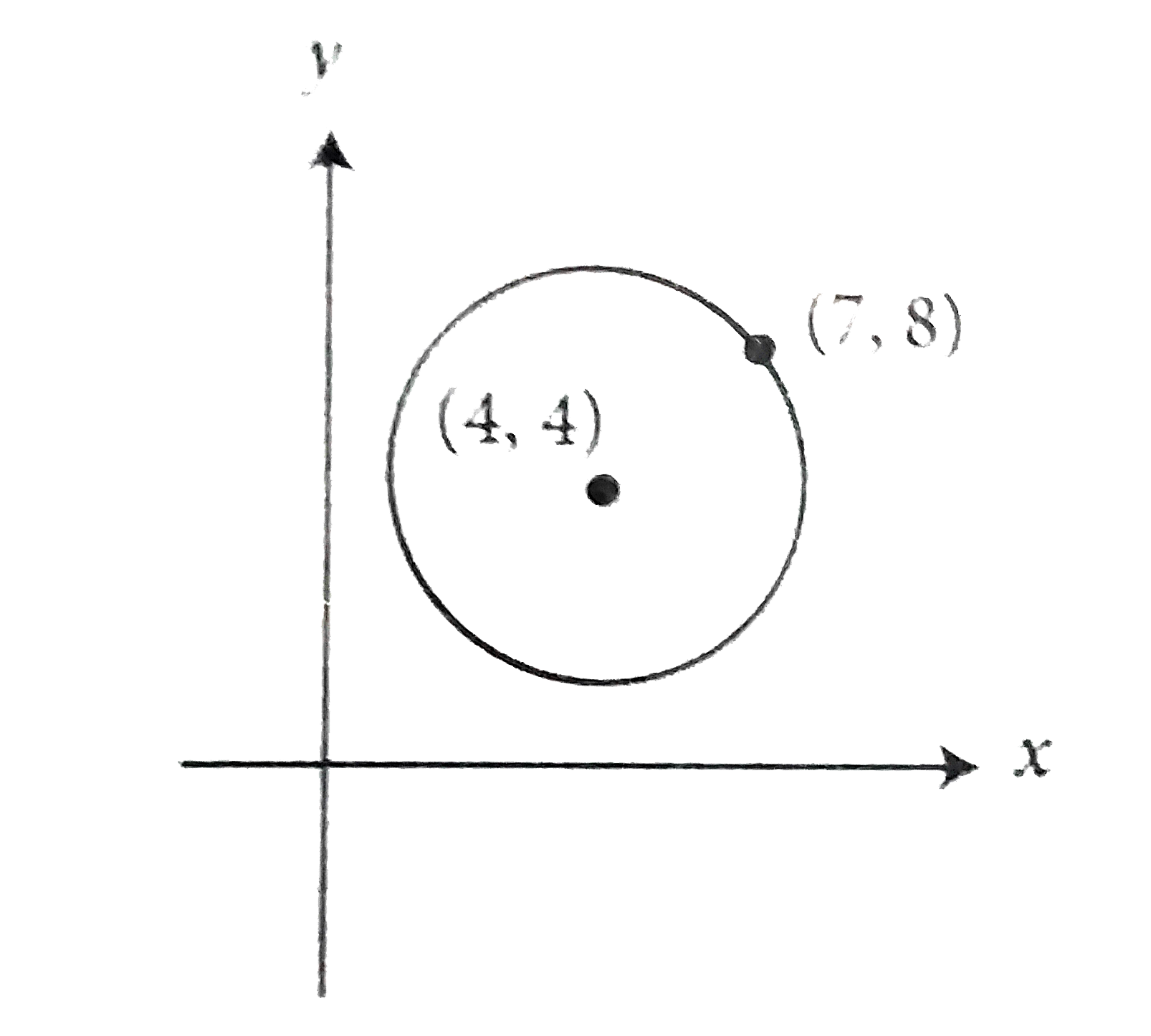
the circle defined by the equation (x−4)2+(y−4)2=25 has its centre at point (4,4) and includes point (7,8) on the circle. This is shown in the figure above. What is the area of the circle shown?A5πB10πC16πD25π
The equation of the circle concentric with x2+y2−6x+4y−3=0 and having radius 5 is
View SolutionFind the equation of the circle the end points of whose diameter are the centres of the circle : x2+y2+6x−14y=1 and x2+y2−4x+10y=2.
View SolutionIn the xy-plane, the graph of 2x2−6x+2y2=45 is a circle . What is the radius of the circle ?
View SolutionIn the xy-plane , a circle with center (6,0) is tangent to the line y=x. what is the radius of the circle ?
View Solutionx2+y2+8x−20y=28
What is the diameter of the circle given by the equation above ?
View Solution
