The total cost, y for Rosa to go on vacation for x days given by the equation y=A+(H+M)x, where A represents the airface, H represents the cost per day for the hotel, and M represents the cost the metal. If the relationship between the total cost of the vacation and the number of the days of the vacation is graphed on the xy-plane, what does the slope of the line represents?
The total cost daily cost of the hotel and meals
The total daily cost of the vacation
The total cost of the hotel and meals
The total cost of the vacation
The correct Answer is:A
To solve the problem step by step, we will analyze the equation given and determine what the slope of the line represents in the context of the vacation costs.
Step 1: Understand the equation
The total cost y for Rosa to go on vacation for x days is given by the equation:
y=A+(H+M)x
where:
- A = airfare (fixed cost)
- H = cost per day for the hotel
- M = cost per day for meals
Step 2: Identify the components of the equation
In this equation, (H+M)x represents the variable cost that depends on the number of days x. The term A is a constant that does not change with the number of days.
Step 3: Rewrite the equation in slope-intercept form
The slope-intercept form of a linear equation is given by:
y=mx+c
where m is the slope and c is the y-intercept.
In our equation:
- The slope m can be identified as H+M.
- The y-intercept c is A.
Step 4: Interpret the slope
The slope H+M represents the total cost incurred per day for the hotel and meals combined. This means that for each additional day x that Rosa stays on vacation, her total cost y increases by H+M.
Conclusion
Thus, the slope of the line represents the total daily cost of the hotel and meals.
Final Answer
The slope of the line represents the total daily cost of the hotel and meals, which corresponds to option (a).
---
The total cost y for Rosa to go on vacation for x days is given by the equation:
y=A+(H+M)x
where:
- A = airfare (fixed cost)
- H = cost per day for the hotel
- M = cost per day for meals
In this equation, (H+M)x represents the variable cost that depends on the number of days x. The term A is a constant that does not change with the number of days.
The slope-intercept form of a linear equation is given by:
y=mx+c
where m is the slope and c is the y-intercept.
- The slope m can be identified as H+M.
- The y-intercept c is A.
The slope H+M represents the total cost incurred per day for the hotel and meals combined. This means that for each additional day x that Rosa stays on vacation, her total cost y increases by H+M.
Thus, the slope of the line represents the total daily cost of the hotel and meals.
The slope of the line represents the total daily cost of the hotel and meals, which corresponds to option (a).
Topper's Solved these Questions
Similar Questions
If x=14−y, what is 3x when y=11?
01:09View SolutionIF 3y=y+2, what is the value of 2y?
01:37View SolutionJoy plants three rows of corn in her garden. The row on the south edge of the garden receives more sunlight than the row on north edge of the garden. Therefore, the corn on the north edge the south edge of the garden is 30% shorter than that on the south. If the corn on the south edge of the garden is 50 inches tall, how tall is the corn on the north edge of the garden , in inches?
04:34View SolutionThe cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.(Take the cost of a notebook to be Rs x and that of a pen to be Rs y).
View SolutionThe cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement. (Take the cost of a notebook to be x and that of a pen to be? y).
02:47View Solutiony = 19.99 + 1.50x
The equation above models the total cost y, in dollars, that a company charges a customer to rent a truck for one day and drive the truck x miles. The total cost consists of a flat fee plus a charge per mile driven. When the equation is graphed in the xy-plane, what does the y-intercept of the graph represent in terms of the model?02:53View SolutionMr. Martinson is building a concrete patio in his backyard and deciding where to buy the materials and rent the tools needed for the project. The table below shows the materials’ cost and daily rental costs for three different stores.

The total cost, y, for buying the materials and renting the tools in terms of the number of days, x, is given by y=M+(W+K)x .
If the relationship between the total cost, y, of buying the materials and renting the tools at Store C and the number of days, x, for which the tools are rented is graphed in the xy-plane, what does the slope of the line represent?03:23View SolutionThe cost of using a telephone in a hotel meeting room is $0.20 per minute. Which of the following equations represents the total cost c, in dollars, for h hours of phone use?
03:09View Solution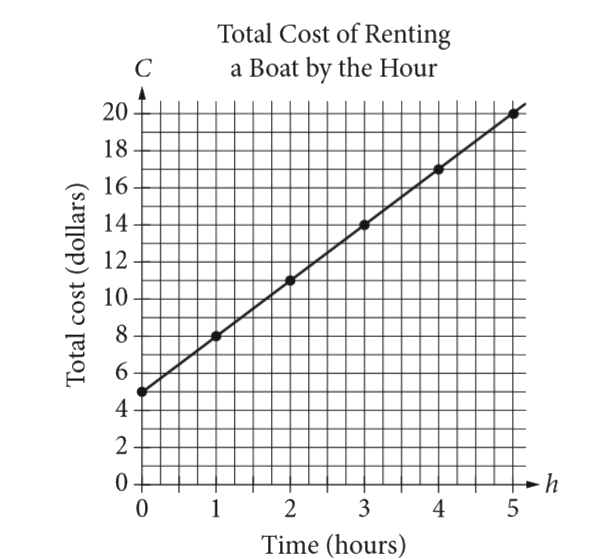
The graph above displays the total cost C, in dollars, of renting a boat for h hours.
What does the C-intercept represent in the graph?01:18View Solution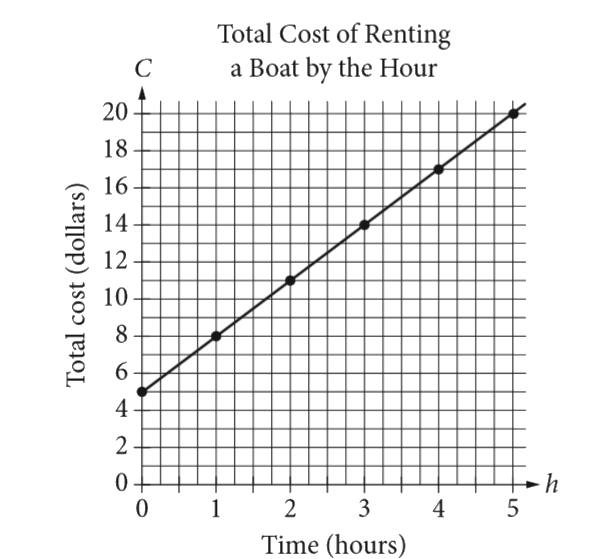
The graph above displays the total cost C, in dollars, of renting a boat for h hours.
Which of the following represents the relationship between h and C ?05:04View SolutionThe curve represented by x = 3 (cost + sint), y = 4(cost – sint) , is
View SolutionThe cost of a notebook is twice, the cost of pen. Write a linear equation in two variables, to represent this statement. (Take the cost of a notebook to be rs. x that of a pen to be rs. Y)
01:30View SolutionA cottage industry produces a fixed number of items every day. The cost of each item made in a day (in rupees) is more than double the number of items made in that day. The total cost of the goods made that day was Rs. Find out the total number of items made that day which is 90 and the cost of each item.
02:52View SolutionWhat is the relationship between total variable cost and marginal cost? Explain.
01:37View SolutionThe cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.(Take the cost of a notebook to be Rs x and that of a pen to be Rs y).
01:46View Solution

