Let IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
IA<IB
IA<IB, whether the axes are parallel or not parallel
if the axes are parallel IA<IB
If the axes are not parallel IA≥IB
The correct Answer is:C
ICM is less than I about any other axis not passing through centre of mass but only when two axes are parallel.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
View SolutionIn the figure shown, a planer body is in the shape of a rhombus ABCD: I1 and I2 are moment of inertias: about axis passing through centre and perpendicular to sides BC and DC respectively. I3 and I4 are amount of inertias about diagonal axis BD and AC respectively. Then the moment of inertia about an axis passing through centre and perpendicular tothe plane of body is given by

View Solution
Knowledge Check
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not
AIA<IBBIf IA<IB the axes are parallelCIf the axes are parallel IA<IBDIf the axes are not parallel the IA>IBLet IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not
AIA<IBBIf IA<IB the axes are parallelCIf the axes are paralel IA<IBDif the axes are not parallel the IA≥IBLet I1 and I2 be the moment of inertia of a uniform square plate about axes APC and OPO respectively as shown in the figure.P is centre of square. The ratio I1I2 moment of inertia is -
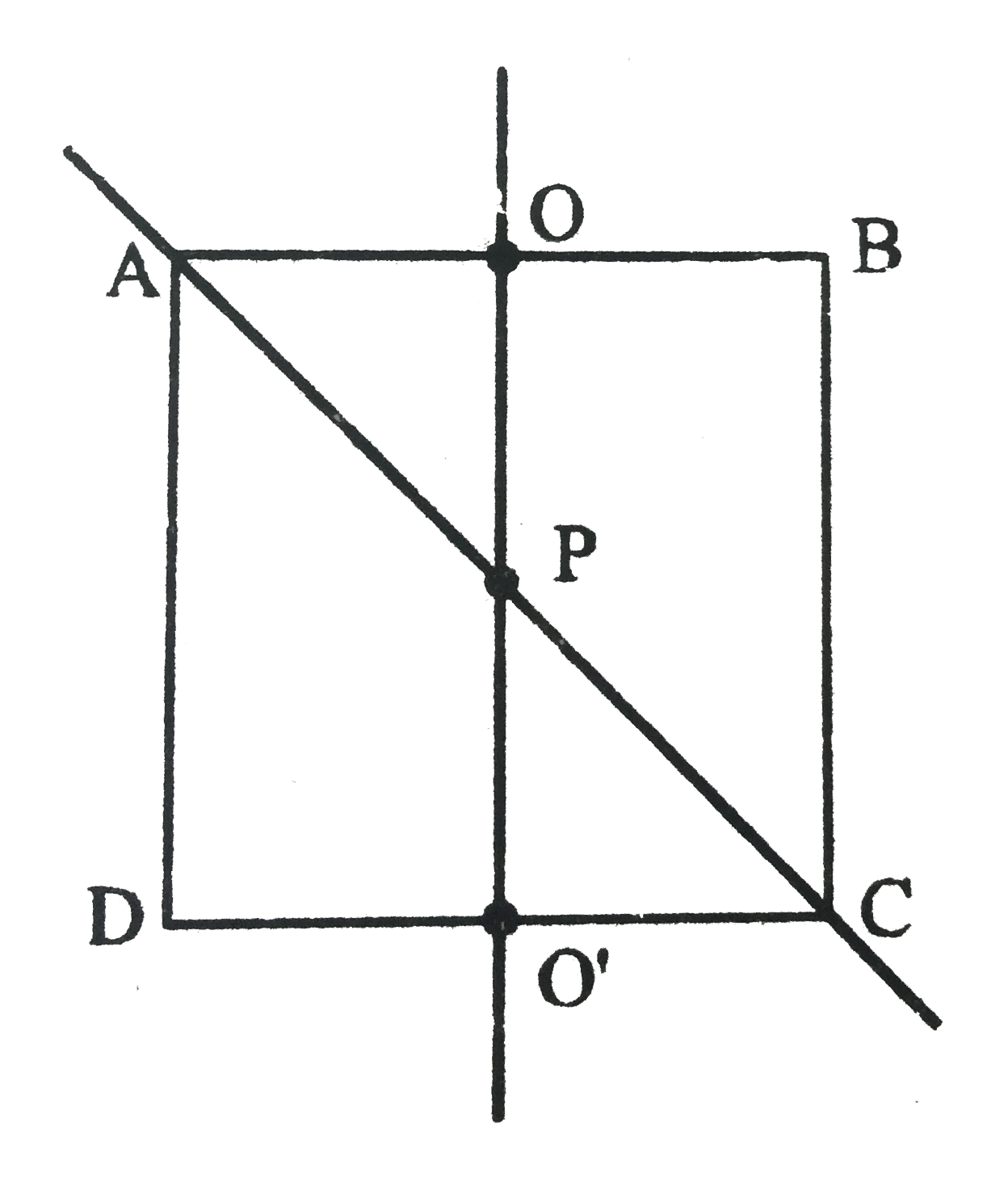 .A12√2B2C12D1
.A12√2B2C12D1
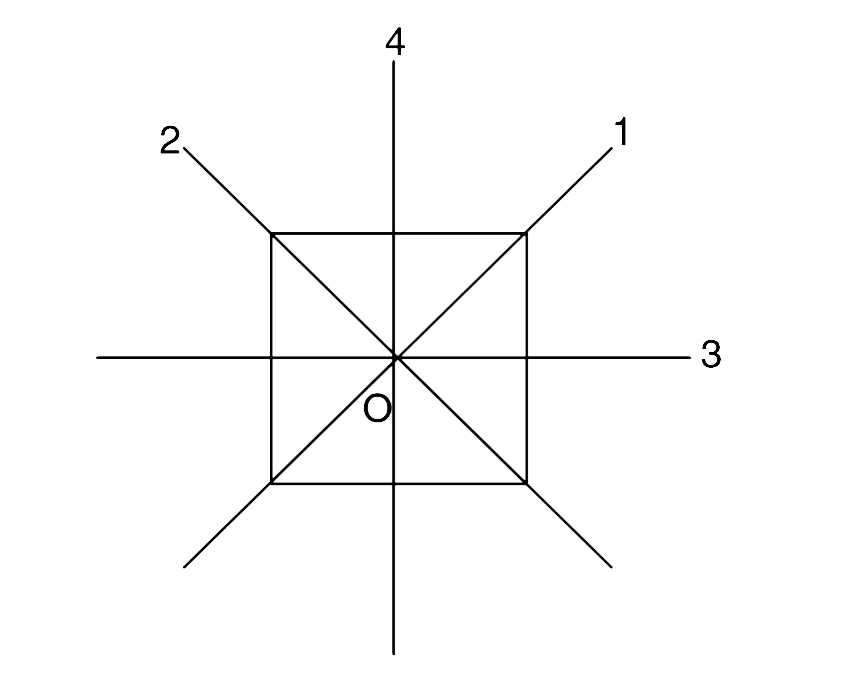
Consider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionMoment of inertia of a rigid body about an axis passing through its centre of mass is I0 and moment of inertia of the same body about another axis parallel to the first axis is I. Then
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mas and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionMinimum moment of inertia of a uniform body is I about and axis. The axis must be passing through COM of body.
Moment of inertia depends on distribution of mass about axis of rotation.
View Solution
