A conical pendulum is moving in a circle with angular velocity ω as shown. If tension in the string is T, which of following equations are correct ?

T=mωt2
Tsinθ=mω2t
T=mgcosθ
T=mω2tsinθ
The correct Answer is:A
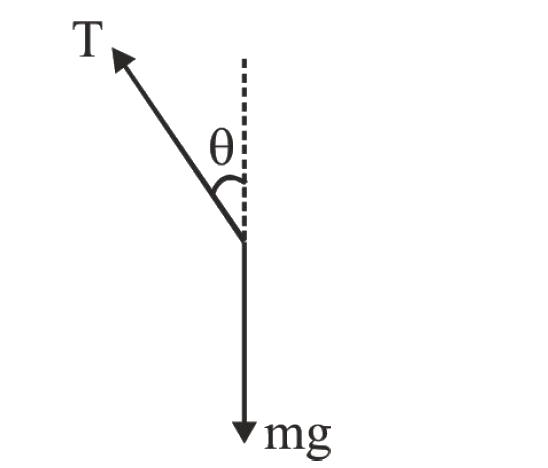
Tcosθ=mg
Tsinθ=mrω2
⇒Tsinθ=mlsinωω2
⇒T=mfω2.
Topper's Solved these Questions
Similar Questions
The tension T in the string shown in figure is
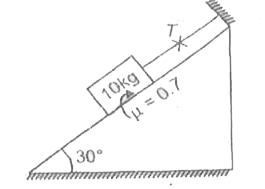 View Solution
View SolutionThe conical pendulum is in steady circular motion with constant angular velocity ω as shown in Fig. Mass of the particle is M and string makes angle α with vertical.
(a) Find angular momentum of the particle about the center C of the circle and the hinge O about which the string is attached.
(b) Also check whether L is changing or is constant.View Solution
Knowledge Check
- Question 1 - Select One
A stone is tied to one end of a steing and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the lrngth of the string is halved and its angular velocity is doubled , the tension in the string will be
A4 TBT/2CT/4D2 T - Question 2 - Select One
A spherical body moves with uniform angular velocity (ω) around a circular path of radius r . Which one of the following statements is correct ?
AThe body has no acceleration.BThe body has a radial acceleration ω2r directed toward centre of path .CThe body has a radial acceleration 25ω2r directed away from the centre of the path .DThe body has an acceleration ω2 tangential to its path . - Question 3 - Select One
A stone of mass M is tied at the end of a string, is moving in a circle of radius R, with a constant angular velocity ω. The total work done on the stone, in any half circle, is:
AπMR2ω2B2MR2ω2CMR2ω2D0
For a particle moving in a horizontal circle with constant angular velocity:
View SolutionA particle of mass m is attached to one end of a weightless and inextensible string of length L. The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other and is attached a small particle of equal mass m. The system is set in motion with the first particle describing a circle on the table with constant angular velocity ω1 and the second particle moving in the horizontal circle as a conical pendulum with constant angular velocity ω2 Show that the length of the portions of the string on either side of the hole are in the ratio ω22:ω21
View SolutionA body of mass m is moving in a circle of radius angular velocity ω. Find the expression for centripetal force acting on it by the method of dimensions
View SolutionIf a small babyof mass m is moving with angular velocity ω in a circle of radius r, then its K.E. will be
View SolutionFor a conical pendulum of string length L, its angular speed is proportional to
View Solution

