Kinetic energy of a particle moving along elliptical trajectory is given by K=αs2 where s is the distance travelled by the particle. Determine dimensions of α
(MLT−2)
(MLT−2)
(ML−1T−2)
(MT−2)
The correct Answer is:D
Step by step video, text & image solution for Kinetic energy of a particle moving along elliptical trajectory is given by K=alpha s^(2) where s is the distance travelled by the particle. Determine dimensions of alpha by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNIT & DIMENSIONSBOOK - MOTIONCHAPTER - UNIT & DIMENSIONSEXERCISE - Exercise - 3 (Level - I) (Section D -Basic Mathematics)
1 Videos
- UNIT & DIMENSIONSBOOK - MOTIONCHAPTER - UNIT & DIMENSIONSEXERCISE - Exercise - 3 (Level - II) (Section A- Units)
1 Videos
- UNIT & DIMENSIONSBOOK - MOTIONCHAPTER - UNIT & DIMENSIONSEXERCISE - Exercise - 3 (Level - I) (Section B- Dimensions)
2 Videos
- ThermodynamicsBOOK - MOTIONCHAPTER - ThermodynamicsEXERCISE - EXERCISE - 3 SECTION b
26 Videos
- UNITS AND DIMENSIONS, BASIC MATHEMATICS BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - PRACTICE QUESTION
4 Videos
Similar Questions
The variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
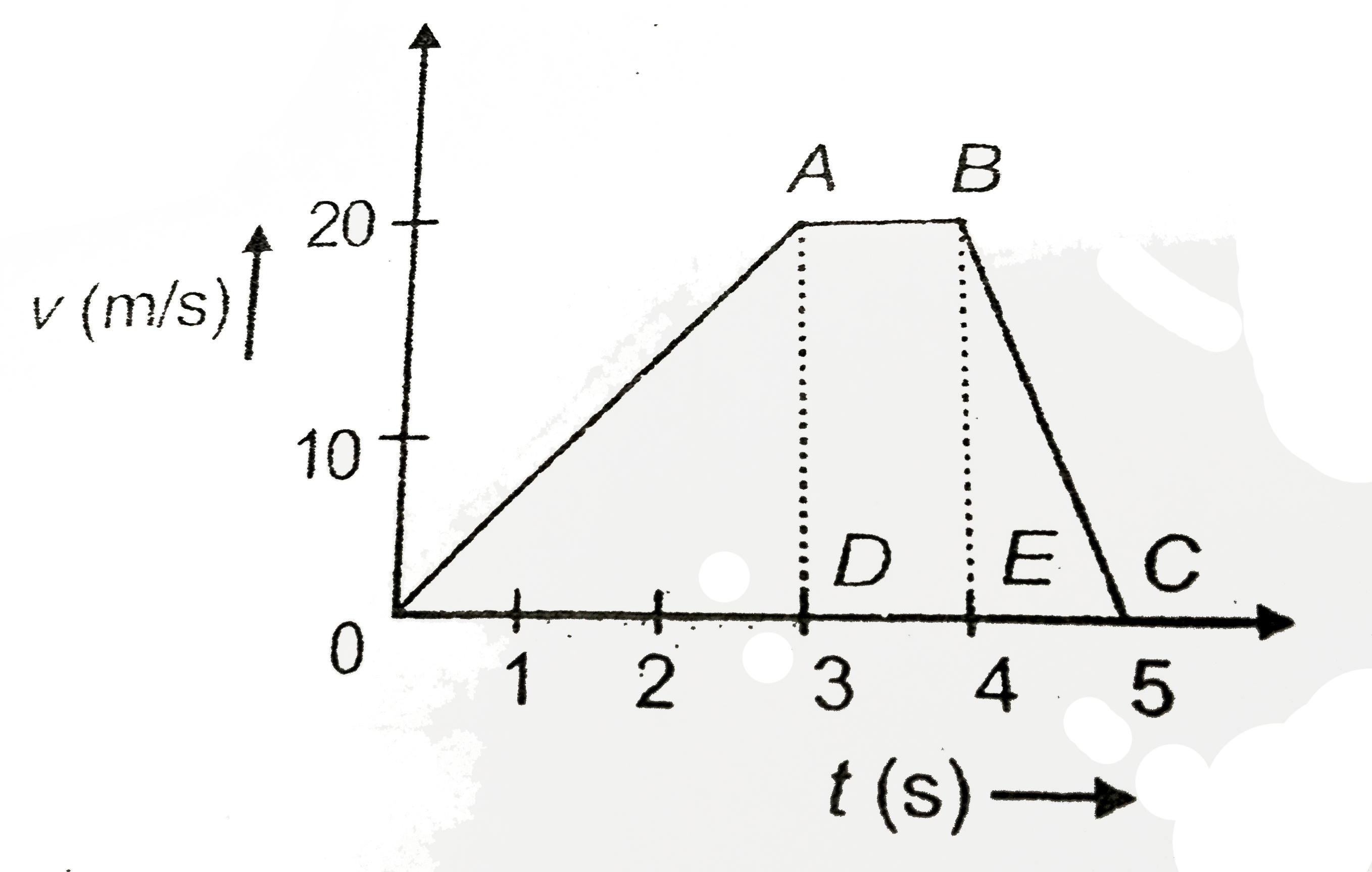
View SolutionThe instantaneous velocity of a particle moving in a straight line is given as v=αt+βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is :
View Solution
Knowledge Check
The variation of velocity of a particle moving along straight line is shown in the figure. The distance travelled by the particle in 4 s is
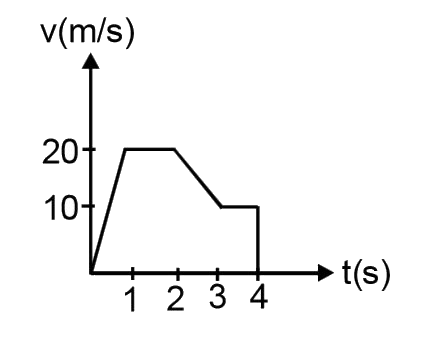 A25mB30mC55mD60m
A25mB30mC55mD60mThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
A(a) 2as2RB(b) 2as[1+s2R]1/2C(c) 2asD(d) 2aKinetic energy of a particle moving along a circle of radisu R depends on the distance covered as K=as2 where a is a constant . Find the force acting on the particle as a function of s.
A2as√1+(sR)2B2as√1+(Rs)2C2as√1+(sR)2D2sa√1+(Rs)2
The kinetic energy of a particle moving along a circle of radius R depends on the distance covered s as K=λs2, where λ is a constant. Find the force acting on the particle as a function of s.
View SolutionThe position of a particle along x-axis at time t is given by x=1−t+t2. The distance travelled by the particle (in 'm') in first 2 seconds is 's'. Fill '2s' in OME sheet.
View SolutionA particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends on the distance covered a as K=as2. The force acting on the particle is
View SolutionThe velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
View Solution
