Consider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure).
In terms of G, Me, m and r find the total mechanical energy EA + EB of the two satellite plus earth system before collision.

Video Solution

Text Solution

Verified by Experts

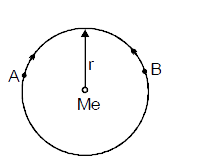
$- G m M_{e} / r$

Updated on:21/07/2023

A satellite whose mass is M , is revolving in circular orbit of radius r around the earth. Time of revolution of satellite is
A $T \propto \frac{r^{5}}{G M}$
B $T \propto \sqrt{\frac{r^{3}}{G M}}$
C $T \propto \sqrt{\frac{r}{G M^{2} / 3}}$
D $T \propto \sqrt{\frac{r^{3}}{G M^{1} / 4}}$
A satellite is revolving in circular orbit of radius $r$ around the earth of mass M. Time of revolution of satellite is
A $T \propto \frac{r^{5}}{G M}$
B $T \propto \sqrt{\frac{r^{3}}{G M}}$
C $T \propto \sqrt{\frac{r}{\frac{G M^{2}}{3}}}$
D $T \propto \sqrt{\frac{r^{3}}{\frac{G M}{4}}}$
The satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. then, its angular momentum will be
A $\sqrt{\frac{E}{m r^{2}}}$
B $\frac{E}{2 m r^{2}}$
C $s q t (2 E m r^{2})$
D $\sqrt{2 E m r}$