A sphere of radius R has its centre at the origin. It has a uniform mass density ρ0 except that there is a spherical hole of radius r=R/2 whose centre is at x=R/2 as in fig (a) find gravitational field at points on the axis for x>R (ii) Show that the gravitational field inside the hole is uniform, find its magnitude and direction.

→g=+πGρ0R36⎡⎢ ⎢ ⎢⎣1(x−R2)2−8x2⎤⎥ ⎥ ⎥⎦,→g=−2πGρ0R3→i
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 3 | Level - II (Subjective | JEE Advanced)10videos
GRAVITATION
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 | Level - I (Previous year | JEE Main)16videos
GRAVITATION
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 2 (Level - II) Multiple choice | JEE Advanced12videos
GRAVITATION
- BOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II55videos
GEOMETRICAL OPTICS
- BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced22videos
HEAT - 1
Similar Questions
A current is passing through a cylindrical conductor with a hole (or cavity) inside it. Show that the magnetic field inside the hole is uniform and find its magnitude and direction.
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View Solution
Knowledge Check
- Question 1 - Select One
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2 - Question 2 - Select One
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2 - Question 3 - Select One
Mass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
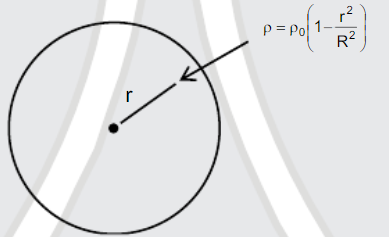 A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.
 View Solution
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
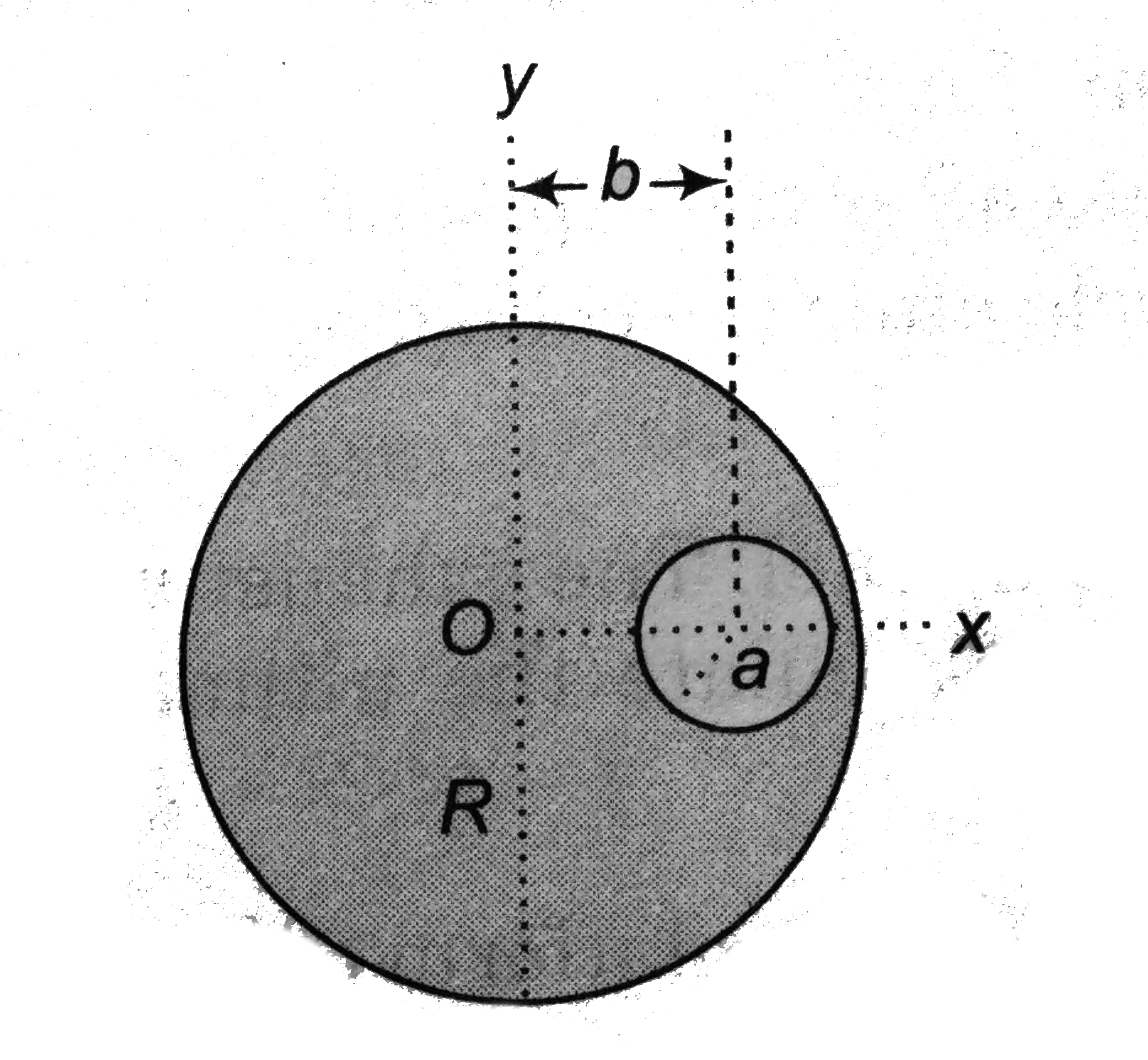
View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
 View Solution
View SolutionA sphere of radius 2R has a uniform charge density p. The difference in the electric potential at r = R and r = 0 from the centre is:
View SolutionA spherical cavity is made inside a sphere of density ρ. If its centre lies at a distacne l from the centre of the sphere, show that the gravitational field strength of the field inside the cavatiy is
E=4π3GlρView Solution

