In a parallelogram as shown in the figure $(a \neq b)$ : equation of the diagonal AC is $(a + b) x + (a + b) y = 3 a b$

Video Solution

Answer

Step by step video & image solution for In a parallelogram as shown in the figure (a != b) : equation of the diagonal AC is (a + b) x + (a + b)y = 3 ab by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DEFAULT

Similar Questions

In a parallelogram as shown in the figure $(a \neq b)$ : equation of the diagonal AC is $(a + b) x + (a + b) y = 3 a b$
View Solution
In a parallelogram as shown in the figure $(a \neq b)$

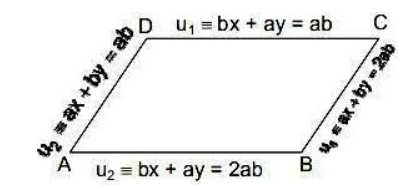
Prove that the equation of the diagonal AC is $(a + b) x + (a + b) y = 3 a b$
View Solution
Let ABCD be a parallelogram the equation of whose diagonals are $A C : x + 2 y = 3$ ; BD: 2x + y = 3. If length of diagonal $A C = 4$ units and area of $A B C D = 8$ sq. units. Find the length of the other diagonal is a. $10 / 3$ b. $2$ c. $20 / 3$ d. None of these
View Solution
ABCD is a parallelogram. x + 2y = 3 and 2x + y = 3 are the equations of the diagonals AC and BD respectively. AC = 4 units and area of parallelogram ABCD is 8 sq. units then The length of BC is equal to
View Solution
Let $A B C D$ be a parallelogram the equation of whose diagonals are $A C : x + 2 y = 3$ ; $B D : 2 x + y = 3$ . If length of diagonal $A C = 4$ units and area of $A B C D = 8$ sq. units. Then
(i) The length of the other diagonal is
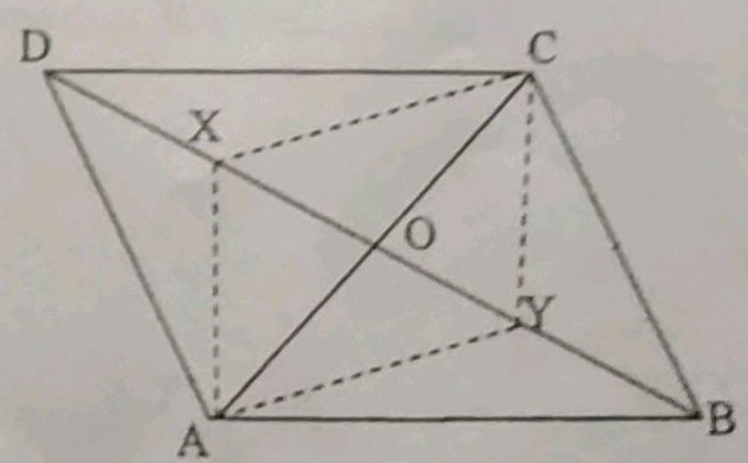
(ii) the length of side $A B$ is equal to
View Solution
In Figure, $A B C D$ is a parallelogram and $X a n d Y$ are points on the diagonal $B D$ such that $D X = B Y$ . Prove that $A X C Y$ is a parallelogram (ii) $A X = C Y, A Y = C X$ $A Y B ≅ C X D$ (iv) $A X D ≅ C Y B$
View Solution
In Figure, $A B C D$ is a parallelogram and $X a n d Y$ are points on the diagonal $B D$ such that $D X = B Y$ . Prove that $A X C Y$ is a parallelogram (ii) $A X = C Y, A Y = C X$ $A Y B ≅ C X D$ (iv) $A X D ≅ C Y B$

View Solution
$3 x - 2 y + 1 = 0 and 2 x - y = 0$ are the equation of the sides $A B and A D$ of the parallelogram $A B C D$ and the equation of a diagonal of the parallelogram is $5 x - 3 y - 1 = 0$ . The equation of the other diagonal of the parallelogram is : (A) $x - y + 1 = 0$ (B) $x - y - 1 = 0$ (C) $3 x + 5 y + 13 = 0$ (D) $3 x + 5 y = 13$
View Solution
Let ABCD be a parallelogram the equation of whose diagonals are $A C : x + 2 y = 3$ ; BD: 2x + y = 3. If length of diagonal $A C = 4$ units and area of $A B C D = 8$ sq. units. (i) The length of the other diagonal is (ii) the length of side AB is equal to
View Solution
In Figure, $A B C D$ is a parallelogram and $X a n d Y$ are points on the diagonal $B D$ such that $D X = B Y$ . Prove that $A X C Y$ is a parallelogram (ii) $A X = C Y, A Y = C X$ (iii) $A Y B ≅ C X D$ (iv) $A X D ≅ C Y B$
View Solution

In a parallelogram as shown in the figure (a≠b) : equation of the diagonal AC is (a+b)x+(a+b)y=3ab

Similar Questions

Recommended Questions

In a parallelogram as shown in the figure $(a \neq b)$ : equation of the diagonal AC is $(a + b) x + (a + b) y = 3 a b$