A particle of mass m moves on the x-axis as follows. It starts from rest at t = 0 from the point x = 0 and comes to rest at t = 1 at the point x = 1 No other information is available about its motion at intermediate time (0<t<1). If α denotes the instantaneous acceleration of the particle, then
Since the body is at rest at x=0 and x=1. Hence α cannot be positive for all time in the interval 0≤t≤1.
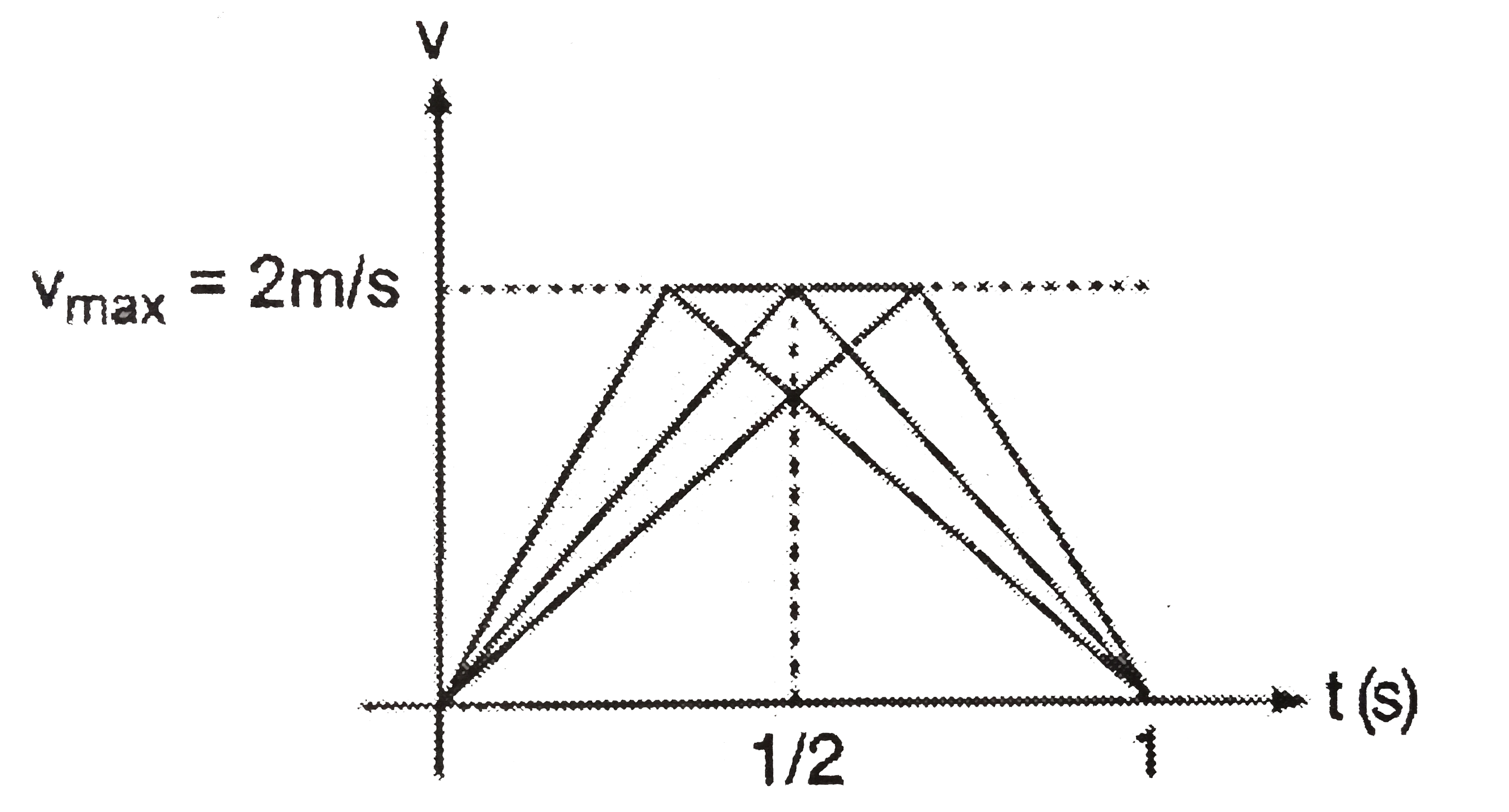
Total time, t=1s. And total displacement, s=1m
s= area under v−t graph
∴ height or vmax=2st=2m/s is fixed (area or s=12×t×vmax)
In case 1 : acceleration >4m/s2 while retardation <4m/s2 and
In case 2: acceleration = retardation =4m/s2
In case 3: acceleration <4m/s2 and retardation >4m/s2
Hence |α|≥4m/s2 at some point or points on its path.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problem14videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice16videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions210videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
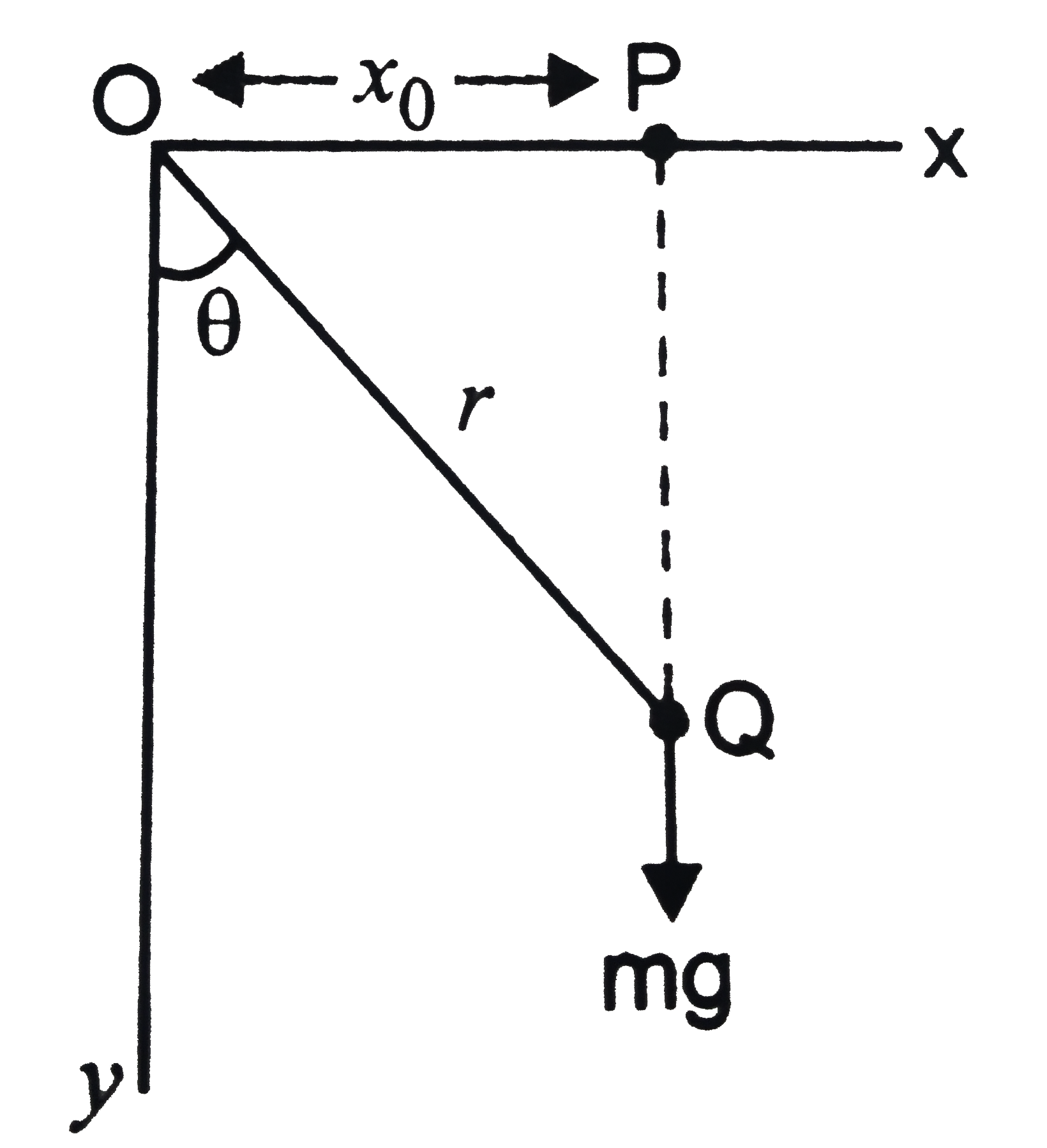
Find the instantaneous velocity of the particle at t=2.5s.View SolutionA particle of mass m is released from rest from point P at x=x0 on X-axis from origin O and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time t, when it is at the point Qw.r.t.O ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle of mass m moves on the x−aξs as follows : it starts from rest at t=0, from the point x=0, and comes to rest at t=l at the point x=1. No other information is available about its motion at intermediate times (0<t<l) . If α denotes the instantaneous accelartion of the particle , then :
Aα cannot remain positive for all t in the interval 0≤t≤1.B|α| cannot exceed 2 at any point in its path .C|α| must be ≥4 at some point or points in its path .Dα must change sign during the motion , but no other assertion can be made with the information given . - Question 2 - Select One or More
A particle of mass m moves on the x-axis as follows: It starts from rest at r= 0 from the pointr=0, and come to rest at 1 at the point x = 1. The velocity changes lincarly with time. No other information is available about its motion at intermediate times [0<t<1] . If α denotes the instantaneous acceleration of the particle , then
Aα cannot remain positive for all t in the interval 0 to 1B|α| cannot exceed 2 at any point in its pathC|α| must be > 4 some point or points in its pathDαmust change sign during the motion, but no other assertion can be made with the given information. - Question 3 - Select One
A point moving along the x- direction starts from rest at x=0 and comes to rest at x=1 after 1 s. Its acceleration at any point is denoted by α . Which of the following is not correct ?
Aα must change sign during the motion.B|α|≥4 units at some or all points during the motion.CIt is not possible to specify an upper limit for |α| from the given data.D|α| cannot be less than 1/2 during the motion.
A point moving along the x-direction starts from rest at x=0 and comes to rest at x=1 after 1 s Its accelertion at any point is denoted by α Which of following is not correct ?
View SolutionA particle is moving under constant acceleration a=kt. The motion starts from rest. The velocity and displacement as a function of time t is
View SolutionA particle moves in a straight line and its position x and time t are related as follows: x=(2+t)1/2
Acceleration of the particle is given byView SolutionA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
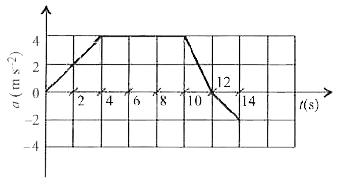 View Solution
View SolutionA particle starts S.H.M. from mean position along straight line and comes to rest momentraily at x = 1 m and t = 1 s. If the motion is simple harmonic, then the maximum acceleration will be (π2=10)
View Solution

