On an incliend plane two particles A and B are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of A and B is cot θ, is the angle at which B is projected measured from. inclined plane, find the angle at which particles are projected.
90∘
60∘
30∘
45∘
The correct Answer is:d
Let B makes an angle α with horizontal.
So γ+α=θ

Topper's Solved these Questions
Similar Questions
On an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
View SolutionFrom an inclined palne two particles P,Q are projected with same speed at same angle θ,one up and other down the plane as shown in figure.Which of the following statement(s) is/are correct ?
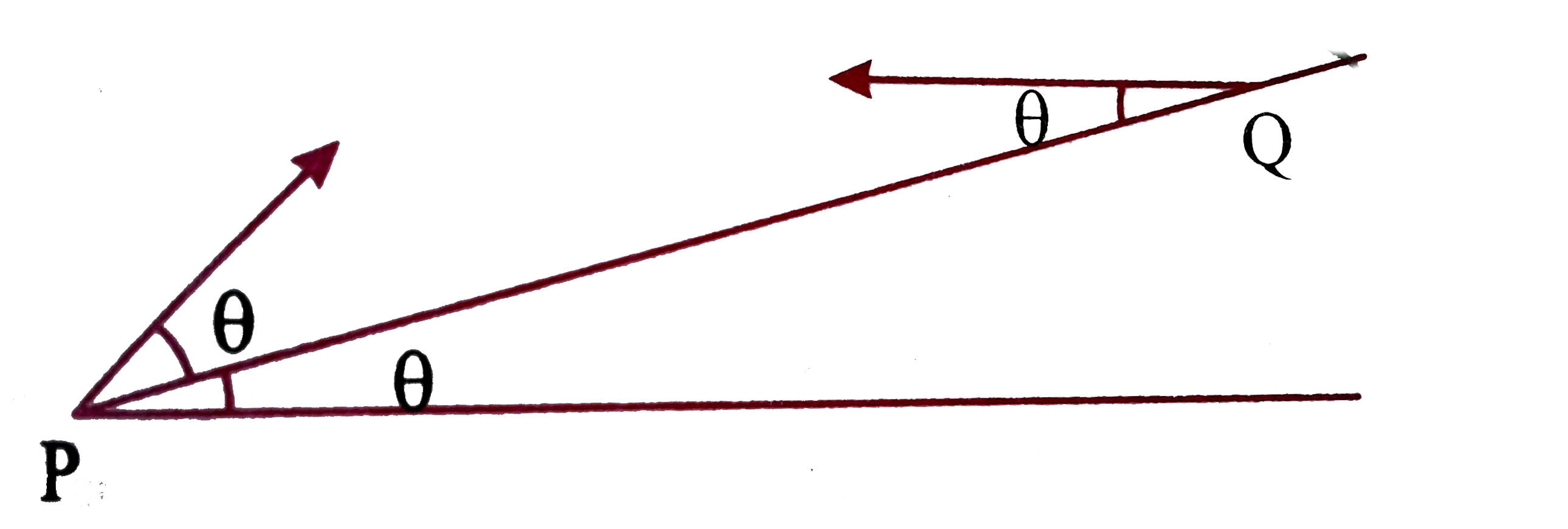
View Solution
Knowledge Check
On an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
A30∘B45∘C15∘D60∘From an inclined palne two particles P,Q are projected with same speed at same angle θ,one up and other down the plane as shown in figure.Which of the following statement(s) is/are correct ?
 AThe particles will collide the plane with same speedBThe times of flight of each particle are sameCBoth particles strike the plane perpendicularlyDThe particles will collide in mid air if projected simultaneuosly and time of flight of each particle is less than the time of collision.
AThe particles will collide the plane with same speedBThe times of flight of each particle are sameCBoth particles strike the plane perpendicularlyDThe particles will collide in mid air if projected simultaneuosly and time of flight of each particle is less than the time of collision.Two particles are projected with same speed but at angles of projection (45∘−θ) and (45∘+θ). Then their horizontal ranges are in the ratio of
A1:2B2:1C1:1Dnone of the above
A particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionAn particle is projected with velocity u on an inclined plane at an angle θ with the plane. If the particle lands on the plane at right Angle and its time of flight is ucosecθ2g. Find the angle of inclination of the plane with horizontal.
View SolutionTwo particles are projected with same velocity but at angles of projection 25° and 65° with horizontal. The ratio of their horizontal ranges is
View SolutionTwo particles are projected simultaneously with same speed V0 in same vertical plane at angle 30∘and60∘ With the horizontal .The time at which their velocities becomes parallel is
View SolutionIf the particle is projected down onto the inclined plane at same speed and angle with the inclined plane the ratio of the time of flight and time of flight for upward projection is :
View Solution
