A block of ice starts sliding down from the top of the inclined roof of a house (angle of inclination of roof= $30^{\circ}$ with the horizontal) along aline of maximum slope. The highest and lowest points of the roof are at heights of 8.1m and 5.6 m respectively from the ground. At what horizontal distance from the starting point will the block hit the ground? Neglect friction.

Video Solution

Text Solution

Verified by Experts

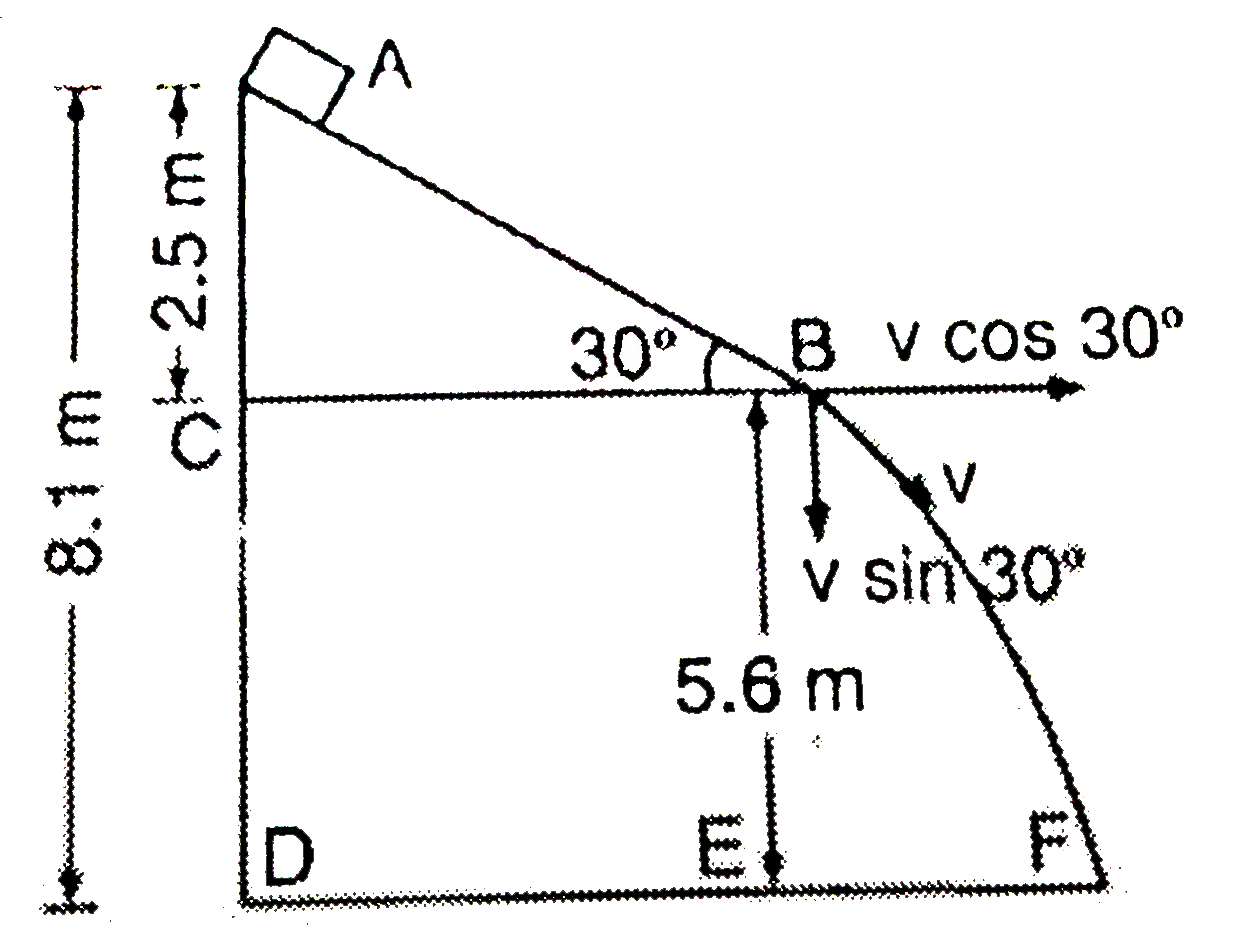
When the ice block silides down from A to B, it falls vertically through AC=2.5m
If v is the velocity with which it reaches B, then $v^{2} = u^{2} + 2 a s$ , where u=0,a= $g {sin 30}^{\circ}$ and s=AB.
$∴ v^{2} = 2 g \times \frac{A C}{A B} \times A B ({sin 30}^{\circ} = \frac{A C}{A B})$
$= 2 \times 9.8 \times 2.5 = 49$
$∴ v = 7 m s^{- 1}$ along AB, Resolve this velocity v into:
(i) a horizontal component
$= v {cos 30}^{\circ} = 7 \times (\sqrt{3} / 2) = 3.5 \times \sqrt{3} m s^{- 1}$
Vertical motion:
Let t be the time taken by the block to reach the ground.
Apply $s = u t + \frac{1}{2} g t^{2}$
Given $s = 5.6 m, u = 3.5 m s^{- 1}, g = 9.8 m s^{- 2}$
$∴ 5.6 = 3.5 t + \frac{1}{2} \times 9.8 t^{2}$ or $4.9 t^{2} + 3.5 t - 5.6 = 0$
Dividing this equation by 0.7, we get $7 t^{2} + 5 t - 8 = 0$
$∴ t = \frac{- 5 + 0 \sqrt{{(5)}^{2} + (4 \times 7 \times 8)}}{2 \times 7}$
$∴ t = \frac{- 5 \pm 15.78}{14}$
Rejecting the -ve value,
$= \frac{- 5 + 15.78}{14} = \frac{10.78}{14} = 0.77 s$
Horizontal Motion:
Horizontal distance travelled EF
=Horizontal velocity xx time
$= 3.5 \times \sqrt{3} \times 0.77 = 4.668 m$
$∴$ Total horizontal distance =DF=DE+EF
$= 4.33 + 4.668 = 8.998 m$
$(D E = B C = A C {cot 30}^{\circ} = 2.5 \times \sqrt{3} = 4.33 m)$

Updated on:21/07/2023

A ball is thrown from a point in level with velocity $u$ and at a horizontal distance $r$ from the top of a tower of height $h$ .
At what horizontal distance $x$ from the foot of the tower does the ball hit the ground ?
A $\frac{u cos θ}{g} {{(u^{2} {sin}^{2} θ + g h)}^{1 / 2} - u sin θ}$
B $\frac{u cos θ}{g} {{(u^{2} {cos}^{2} θ + 2 g h)}^{1 / 2} - u cos θ}$
C $\frac{u cos θ}{g} {{(u^{2} {cos}^{2} θ + g h)}^{1 / 2} - u cos θ}$
D $\frac{u cos θ}{g} {{(u^{2} {cos}^{2} θ + g h)}^{1 / 2} - u cos θ}$
A boy playing on the roof of a $10 m$ high building throws a ball with a speed of $10 m / s$ at an angle of $30 (\circ)$ with the horizontal. How far from the throwing point will the ball be at the height of $10 m$ from the ground ?
$[g = 10 m / s^{2}, {sin 30}^{\circ} = \frac{1}{2}, {cos 30}^{\circ} = \frac{\sqrt{3}}{2}]$
A $5.2 m$
B $4.33 m$
C $2.66 m$
D $8.66 m$
A block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g $= 10 m / s^{2}$ )
A $\sqrt{3}$
B $\frac{1}{\sqrt{3}}$
C $\sqrt{2}$
D $\sqrt{5}$