A swimmer wishes to cross a river 500m width flowing at a rate u. his speed w.r.t. still water is v. for this he makes an angle θ with the vertical as shown in the given figure then:
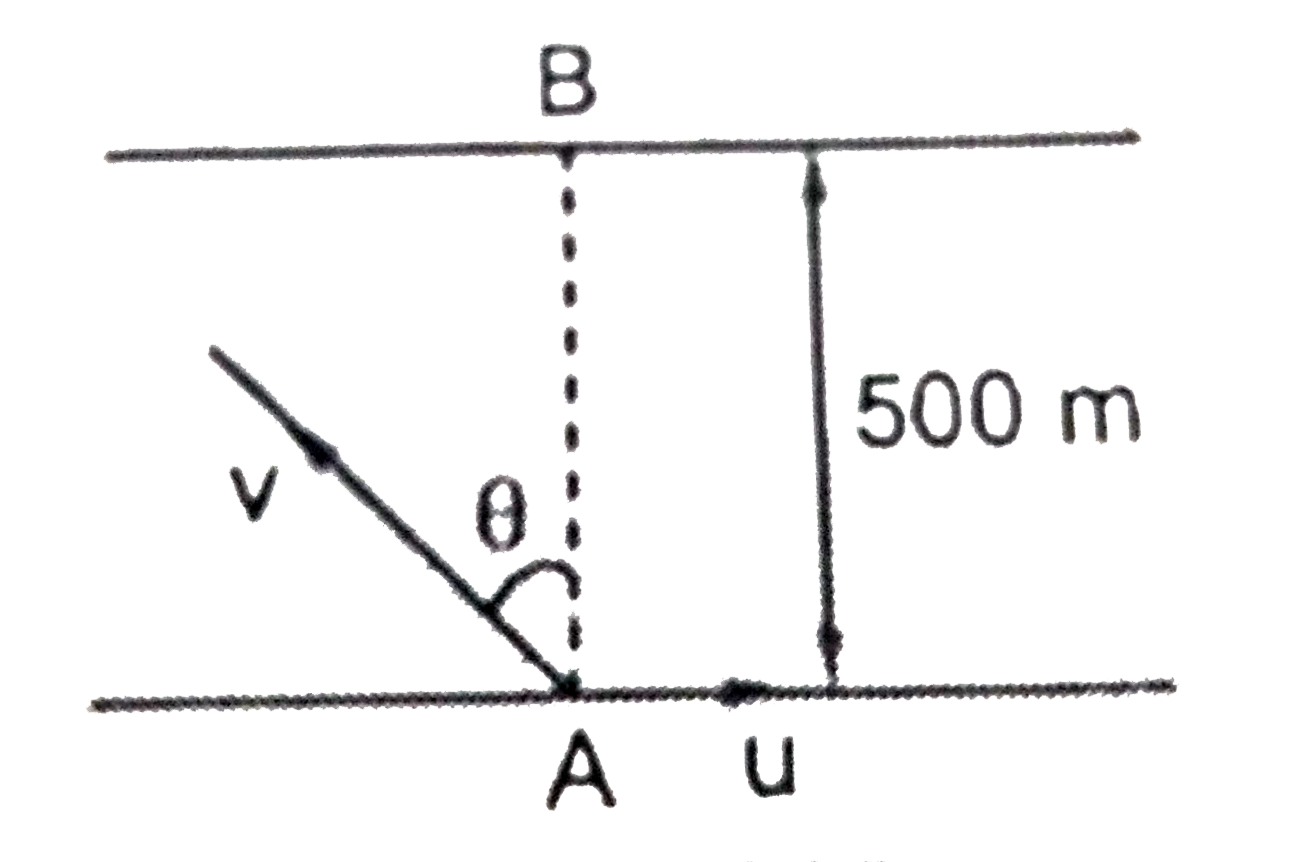
to cross the river in minimum time θ=0∘
to cross the river in minumum time, θ=30∘
for u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.
for u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
The correct Answer is:a,c
t=(ducosθ) for minimum time θ=0.
Topper's Solved these Questions
Similar Questions
A swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. His speed with respect to water is 3km/hr. (a) If the heads in a direction making an angle θ with the flow, he takes to cross the river. (b) Find the shortest possible time to cross the river.
View SolutionA swimmer wishes to cross a 500m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View Solution
Knowledge Check
A swimmer whishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle θ with the perpendicular as shown in the figure.

For u = 5 km/hrand v=3km//hr, the swimmer :ACan reach B in 7.5 min.BCan reach B in 6 min.CCan reach B in less than 6 minDCan never reach BA swimmer wishes to .cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angleθ with the perpendicular as shown ip. the. figure.
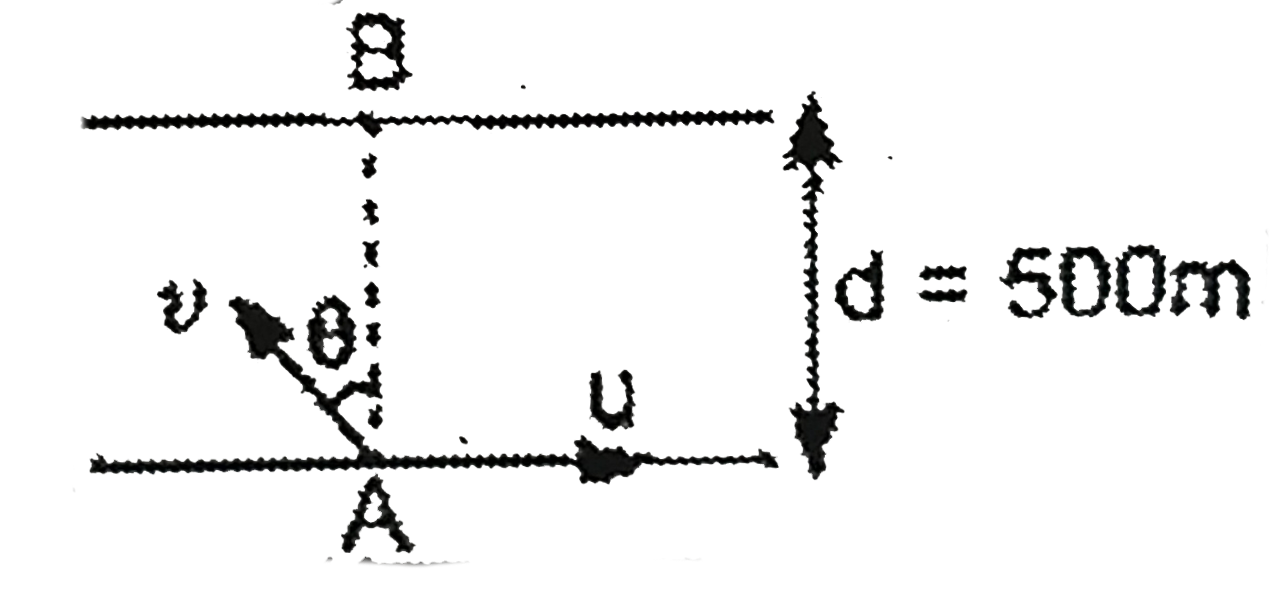
To cross the river in minimum time, the value of θ should be:A0∘B90∘C30∘D60∘A swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
A10minB20minC6minD7.5min
A swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
View Solution
