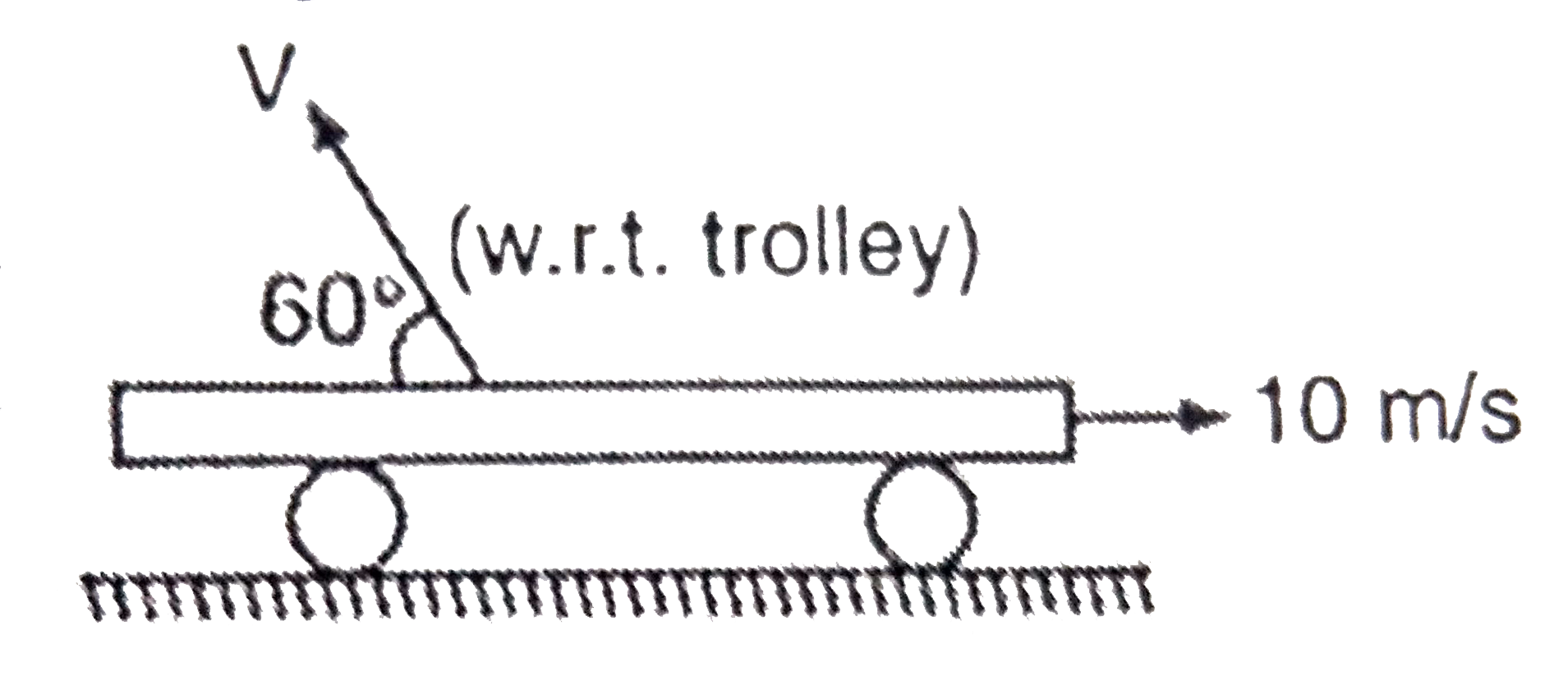
A particle is projected from a stationary trolley. After projection, the trolly moves with velocity 2√15 m/s. for an observer on the trolley, the direction of the particle is as shown in the Fig. 5.121 while for the observer on the ground, the ball rises vertically. the maximum height reached by the abll from the trolley is h metre. The value of h will be:
The correct Answer is:3
vx=vcos60∘=2√15m/s

∴v=4√15m/s
uy=vsin60∘
=4√15×√32=2√45m/s
Hmax=v2y2g=4×4520=9m
Topper's Solved these Questions
Similar Questions
A particle is projected from a stationary trolley. After projection, the trolley moves with a velocity 2(√15)m/s. For an observer on the trolley, the direction of the particle is as shown in the figure while for the observer on the ground, the ball rises vertically. The maximum height reached by the ball from the trolley is h meter. The value of h will be .......... .
 View Solution
View SolutionA (trolley + child) of total mass 200 kg is moving with a uniform speed of 36 km/h on a frictionless track. The child of mass 20 kg starts running on the trolley from one end to the other (10 m away) with a speed of 10 ms–1 relative to the trolley in the direction of the trolley's motion and jumps out of the trolley with the same relative velocity. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
View Solution
Knowledge Check
- Question 1 - Select One
The direction of projection of particle is shown in the figure for an observer on trolley. An observer on the ground sees the ball rising vertically. The maximum height reached by the ball as seen from the trolley is
 A10mB15mC20mD5m
A10mB15mC20mD5m - Question 2 - Select One or More
A particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
Adisplacement of particle is 100mBvertical component of velocity is 20m/sCvelocity makes an angle tan−1(2) with verticalDparticle is at height of 60m from ground - Question 3 - Select One
A particle of mass 2m is projected at an angle of 45∘ with horizontal with a velocity of 20√2m/s. After 1s explosion takes place and the particle is broken into two equal pieces. As a result of explosion one part comes to rest. Find the maximum height attained by the other part. Take g=10m/s2.
A50 mB25 mC40 mD35 m
A particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA particle is projected from ground with velocity 40√2m at 45∘.At time t=2s
View SolutionA particle is dropped from a height 12 g metre and 4 s after another particle is projected from the ground towards it with a velocity 4gms−1 The time after which the second particle meets first is
View SolutionA particle is dropped from a height 12 g metre and 4 s after another particle is projected from the ground towards it with a velocity 4gms−1 The time after which the second particle meets first is
View SolutionA particle is projected from point A on the ground at an angle θ with horizontal. Another particle is projected from point B simultaneously from height 4H above point A with same velocity A and B are in the same vertical plane, where H is the maximum height attained by the particle A, Both the particle collide at the same time on the ground. Find the angle at which particle B is projected with hoizontal.
View Solution

