A (trolley + child) of total mass 200 kg is moving with a uniform speed of 36 km/h on a frictionless track. The child of mass 20 kg starts running on the trolley from one end to the other (10 m away) with a speed of 10 ms–1 relative to the trolley in the direction of the trolley's motion and jumps out of the trolley with the same relative velocity. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
The correct Answer is:9 m/s, 0.9 m
To solve the problem, we will follow these steps:
Step 1: Convert the initial speed of the trolley
The initial speed of the trolley is given as 36 km/h. We need to convert this speed into meters per second (m/s).
Speed in m/s=36×10003600=10 m/s
Step 2: Calculate the initial momentum of the system
The total mass of the trolley and child is 200 kg. The mass of the child is 20 kg. Therefore, the total mass of the system is:
Total mass=200 kg+20 kg=220 kg
The initial momentum P1 of the system is given by:
P1=Total mass×Initial speed=220 kg×10 m/s=2200 kg m/s
Step 3: Determine the final speed of the trolley
Let V be the final speed of the trolley after the child runs to the other end and jumps off. The child runs at a speed of 10 m/s relative to the trolley, so the speed of the child relative to the ground when he jumps off will be:
Child's speed=V+10 m/s
The final momentum P2 of the system when the child is running is given by:
P2=Mass of trolley×V+Mass of child×(V+10)
Substituting the masses:
P2=200V+20(V+10)=200V+20V+200=220V+200
Step 4: Apply the conservation of momentum
Since there are no external forces acting on the system, we can apply the conservation of momentum:
P1=P2
Substituting the values we calculated:
2200=220V+200
Step 5: Solve for V
Rearranging the equation gives:
2200−200=220V
2000=220V
V=2000220≈9.09 m/s
Step 6: Calculate the distance moved by the trolley
The child runs a distance of 10 m at a relative speed of 10 m/s. The time t taken for the child to run from one end of the trolley to the other is:
t=DistanceRelative speed=10 m10 m/s=1 s
Now, we can calculate the distance moved by the trolley during this time at its final speed V:
Distance moved by trolley=V×t=9.09 m/s×1 s≈9.09 m
Final Answers
- The final speed of the trolley is approximately 9.09 m/s.
- The trolley has moved approximately 9.09 m from the time the child begins to run.
The initial speed of the trolley is given as 36 km/h. We need to convert this speed into meters per second (m/s).
The total mass of the trolley and child is 200 kg. The mass of the child is 20 kg. Therefore, the total mass of the system is:
Let V be the final speed of the trolley after the child runs to the other end and jumps off. The child runs at a speed of 10 m/s relative to the trolley, so the speed of the child relative to the ground when he jumps off will be:
Since there are no external forces acting on the system, we can apply the conservation of momentum:
Rearranging the equation gives:
2000=220V
V=2000220≈9.09 m/s
The child runs a distance of 10 m at a relative speed of 10 m/s. The time t taken for the child to run from one end of the trolley to the other is:
- The final speed of the trolley is approximately 9.09 m/s.
- The trolley has moved approximately 9.09 m from the time the child begins to run.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 3 Level-II16videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-I18videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)28videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II19videos
Capacitance
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 416videos
CIRCULAR MOTION
Similar Questions
A trolly of mass 200kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20kg runs on the trolly from one end to the other (10m away) with a speed of 4m/s relative to the trolly in a direction opposite to the trolly's motion and jumps out of the trolly. How much has teh trolly moved from the time the child begins to run ?
View SolutionA trolley of mass 300 ks carrying a sand bag of 25 kg is moving uniformly with a speed of 27km/h on a frictionless track. After a while, sand starts leaking out of a hole on the trolley's floor at the rate of 0.05kgs−1. What is the speed of the trolley after the entire sand bag is empty ?
View Solution
Knowledge Check
- Question 1 - Select One
A trolley having mass of 200kg moves with uniform speed of 36kmh−1 on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4ms−1 relative to the trolley in a direction opposite to its motion and ultimately jumps out of the trolley. with how much velocity has the trolley moved from the time the child begins to run?
A10.36ms−1B11.36ms−1C12.36ms−1D14.40ms−1 - Question 2 - Select One
A child is sitting at one end of a long trolley moving with a uniform speed v on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed u (w.r.t. trolley), the speed of the centre of mass of the system will.
Au+vBv - uCvDnone - Question 3 - Select One
A child is standing at one end of a long trolley moving with a speed v on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed u, the centre of mass of the system (trolley + child) will move with a speed :
AZeroB(v+u)C(v−u)Dv
A child is sitting at one end of a long trolley moving with a uniform speed v on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed u (w.r.t. trolley), the speed of the centre of mass of the system will.
View SolutionA boy of mass m is riding on a trolley of mass M which is moving on smooth floor at speed v0. He jumps off in the opposite direction of motion of trolley with velocity u relative to the trolley before the jump. Find the velocity of the trolley after jump.
View SolutionA pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination α with acceleration a0 is
 View Solution
View SolutionA trolley of mass 8 kg is standing on a frictionless surface inside which an object of mass 2kg is suspended .A conatant force F starts acting on the trolley ,as a result of which the string stood at an angle of 37∘ from the vertical (bob at rest relative to troley ) then,
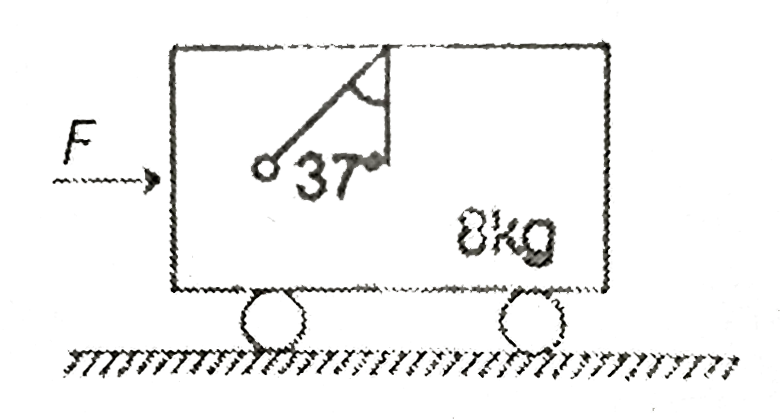 View Solution
View SolutionA boy projects a stone vertically perpendicular to the trolley car with a speed v. If the trolley car moves with a constant velocity u, the time of flight of the stone is :
View Solution

