In the situation shown in figure, both the pulleys and the strings are light and all the surfaces are frictionless. The acceleration of mass M, tension in the string PQ and force exerted by the clamp on the pulley, will respectively be - 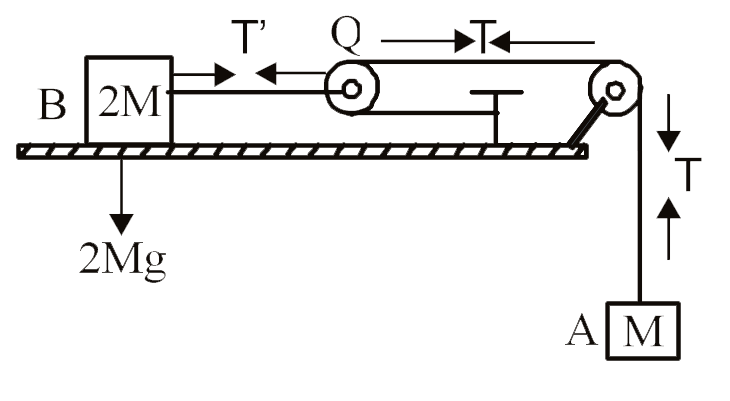
As pulley Q is not fixed, so if it moves a distance d the length of string between P and Q will change by 2d (d from above and d from below), i.e., M will move 2d This in turn implies that if a(→2d) is the acceleration of M, the acceleration of Q and of 2M will be (a/2)(→d)
Now if we consider the motion of mass M, it is accelerated downward, so
T=M(g−a) ....(i)
and for the motion of Q,
2T−T'=0×(a/2)=0,i.e.T'=2T ...(ii)
and for the motion of mass 2M
T'=2M(a/2)i.e.,T'=Ma ...(iii)
From Eqns. (ii) and (iii) as T=(1/2)Ma so Eqn. (i) reduces to
(1/2)Ma=M(g−a)ora=(2/3)g
So, the acceleration of mass M is (2/3) g while tension in the string PQ from Eqn (i) will be,
T=M[g−(2/3)g]=(1/3)Mg
Now from (b) it is clear that force on pulley by the clamp will equal and opposite to the resultant of T and T at 90∘ to each other, i.e.,
(R2)=√T2+T2=√2T=(√2/3)Mg
Note: In this problem the acceleration of pulley Q or mass 2M will be a/2=(1/3) g and tension in the string connecting 2M to the pulley Q, T' will be 2T=(2/3)Mg
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice30videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions134videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice35videos
BASIC MATHEMATICS
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
Similar Questions
Consider the situation shown in figure. Both the pulleys and the strings are light and all the surfaces are frictionless. Calculate
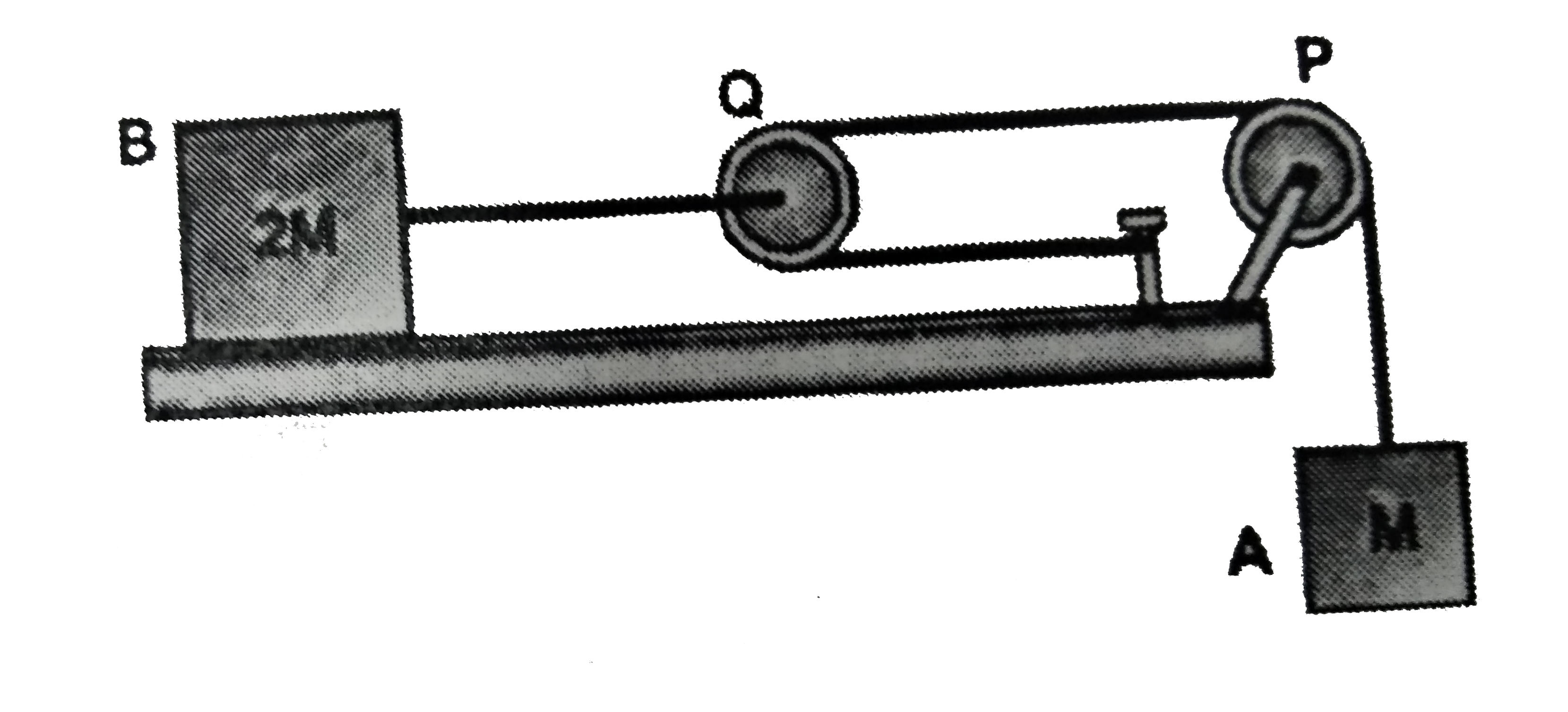
(a) the acceleration of mass M,
(b) tension in the string PQ and
(c ) force exerted by the pulley P.View SolutionConsider4 the situation shown in figure. Bothe the pulleys and the string are light and all the surfaces are friction less. a. Find the acceleration of the mass M. b. Find the tension in the string c. Calculate the force exerted by the clamp on the pulley A in the figure.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Consider the system as shown in the figure. The pulley and the string are light and all the surfaces are frictionless. The tension in the string is (g=10m/s2) .
 A0NB1NC2ND5N
A0NB1NC2ND5N - Question 2 - Select One
Consider the system shown in figure. The pulley and the string are light and all the surface are frictionless. The tension in the string is (Take g=10m/s2)
 A0NB1NC2ND5N
A0NB1NC2ND5N
In the shown arrangement , both pulleys and the string are massless and all the surface are frictionless. Find the acceleration of the wedge.
 View Solution
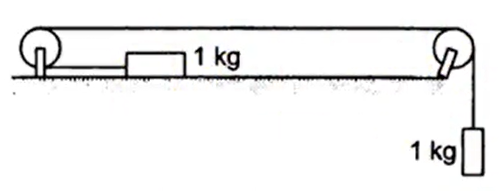
View SolutionCalculate the tension in the string shown in figure. The pulley and the string are light and all surfaces are frictionless. Take g=10 m/s2.
 View Solution
View SolutionConsider the situation shown in figure .Both the pulleys and the string and light and all the surfaces are smooth.
(a) Find the acceleration of 1kg block.
(b) Find the tension in the string. (g=10m/s2).
 View Solution
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.
 View Solution
View SolutionCalculate the tension in the string shown in
(a) The pulleys and the string are light and all surfaces are frictionless. (g=10m/s2)
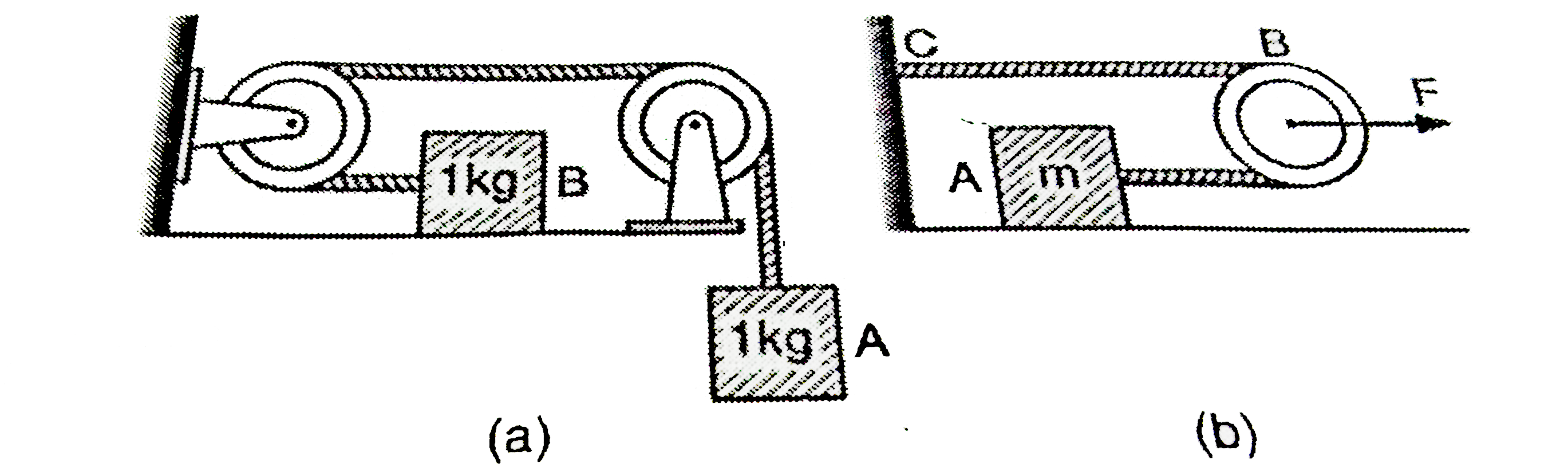 View Solution
View SolutionFind magnitude of force exerted by string on pulley
 View Solution
View Solution

