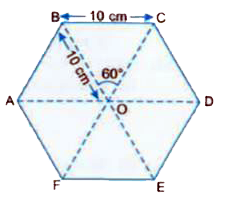
A regular hexagon of side 10 cm has a charge $5 μ C$ at each of its vertices. Calculate the potential at the center of the hexagon.

Video Solution

Text Solution

Verified by Experts

The given figure shows six equal amount of charge, q, at the vertices of a regular hexagon.

Where, Charge q=5 $μ c = 5 \times 10^{- 6} c$
Sid e of the hexagon , I=AB=BC=CD=DE =EF =FA =10 cm
Distance of each vertex from centre O, d= 1 cm
Electric potential at point O
$V = \frac{6 \times q}{4 π \in_{0} d}$
Where,
$\in_{0}$ =permitivity of free space
$\frac{1}{4 π \in_{0}} = \frac{6 \times 9 \times 10^{9} \times 5 \times 10^{- 6}}{0.1}$
$= 2.7 \times 10^{6} V$
Therefore, the potential at the centre of the hexagon is $2.7 \times 10^{6} V$ .

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A hexagon of side 8 cm has a charge $4 μ C$ at each of its vertices. The potential at the centre of the hexagon is
A $2.7 \times 10^{6} V$
B $7.2 \times 10^{11} V$
C $2.5 \times 10^{12} V$
D $3.4 \times 10^{4} V$
Question 2 - Select One
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A $0$
B $\frac{1}{4 π \in_{0}} . \frac{q}{a^{2}}$
C $\frac{1}{4 π \in_{0}} . \frac{6 q}{a^{2}}$
D $\frac{1}{4 π \in_{0}} . \frac{6 q^{2}}{a^{2}}$
Question 3 - Select One
A wire shaped to a regular hexagon of side x carries a current I ampere. Calculate the strength of the magnetic field at the centre of the hexagon.
A $\frac{\sqrt{3} μ_{0} I}{π x}$
B $\frac{3 μ_{0} I}{π x}$
C $\frac{μ_{0} I}{3 π x}$
D $\frac{μ_{0} I}{\sqrt{3} π x}$

NCERT-ELECTROSTATIC POTENTIAL AND CAPACITANCE-Exercise

Home
Ask Doubt
Profile