A thin sheet of metal of uniform thckness is cut into the shape bounded by the line x=a and y=±kx2, as shown. Find the coordinates of the centre of mass
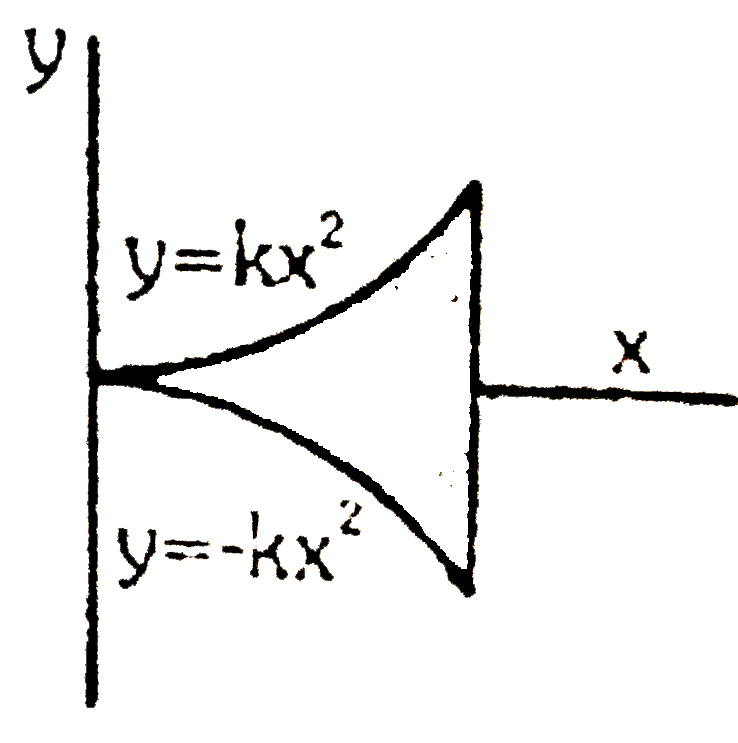
Video Solution
Text Solution
The correct Answer is:34a
|
Answer
Step by step video & image solution for A thin sheet of metal of uniform thckness is cut into the shape bounded by the line x = a and y = +- kx^(2), as shown. Find the coordinates of the centre of mass by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 3 Level-II
16 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-I
18 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)
28 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions
Knowledge Check
From a 16cm×8cm rectangular uniform plane sheet, exactly one quarter of the sheet is removed as shown in figure. If the origin be taken at the centre of the sheet considered as shown in the figure the coordinates of the centre of mass of the remaining sheet is
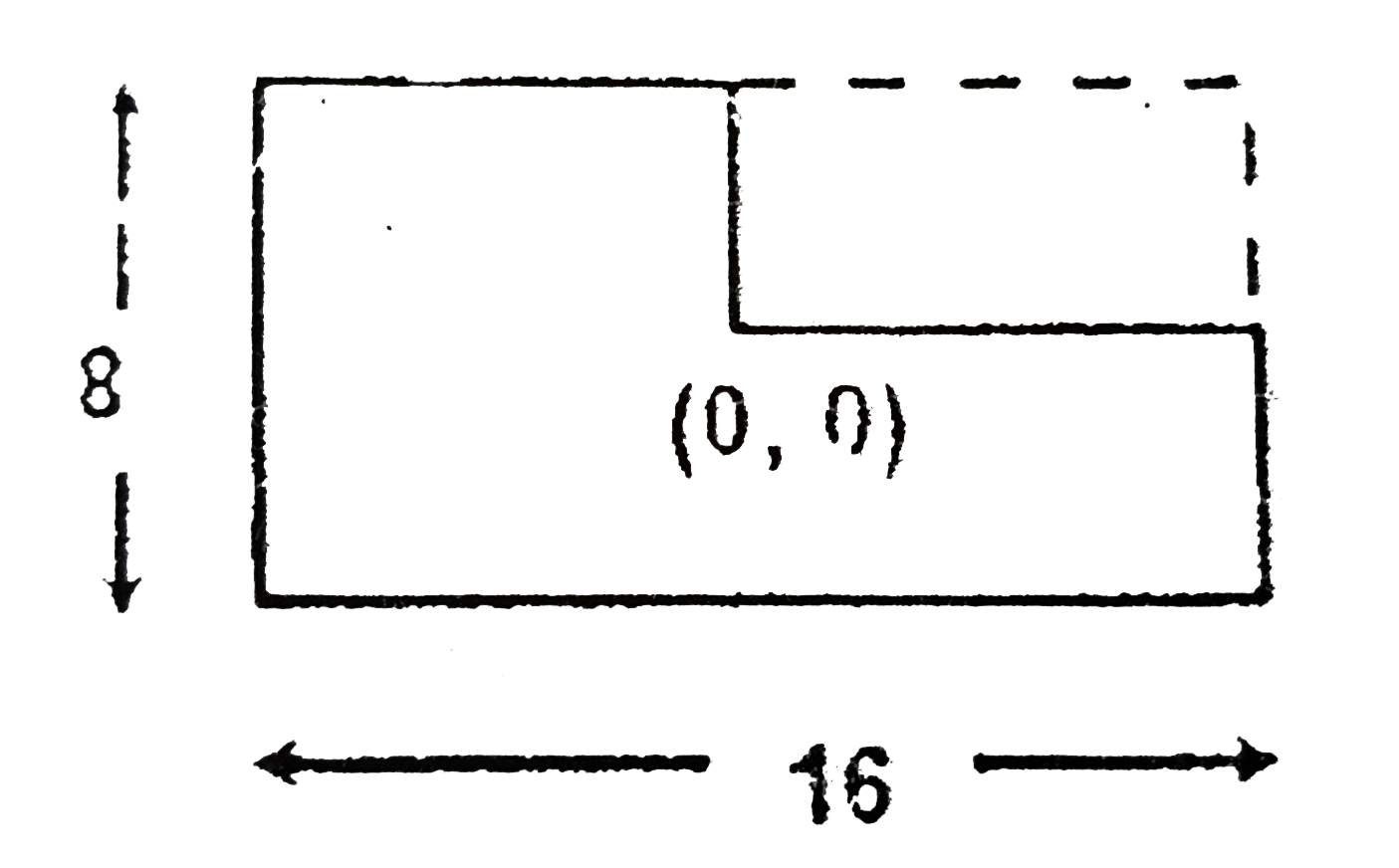 A(4/3,2/3)B(0,2/3)C(4/3,0)D(−4/3,−2/3)
A(4/3,2/3)B(0,2/3)C(4/3,0)D(−4/3,−2/3)A uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
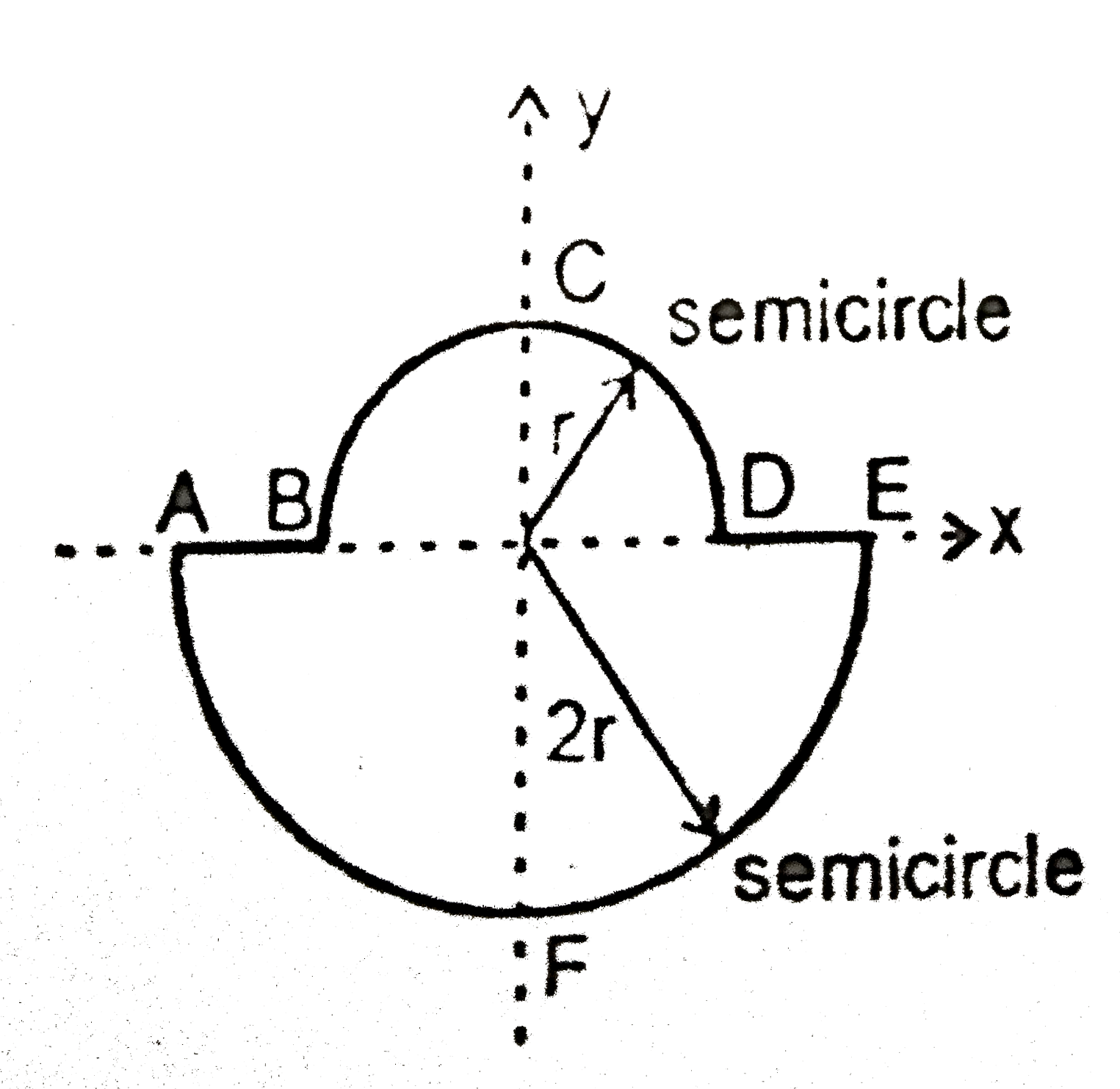 A2rπB−6r3π+2C−2rπDZero
A2rπB−6r3π+2C−2rπDZeroA circle touches both the coordinate axes and the line x−y=√2a,a>0, the coordinates of the centre of the circle cannot be
A(a, a)B(a, -a)C(-a, a)D(-a, -a)
A rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
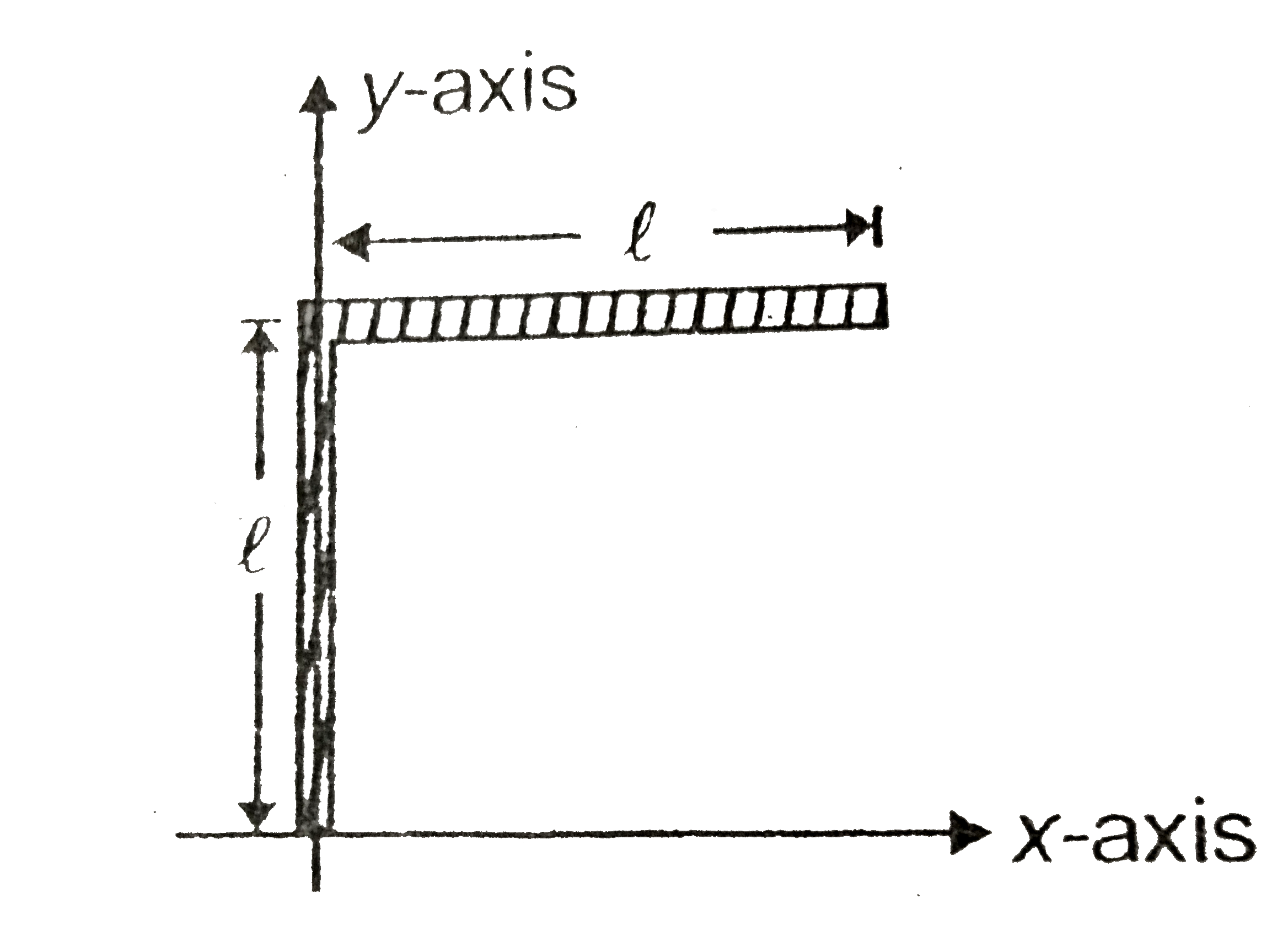
View SolutionFind the area bounded by the curve x2=4yand the line x=4y−2.
View SolutionFind the area bounded by the parabola y=x2 and the line y−2x=2.
View SolutionFind the area bounded by the curves y=log2x and x=2y−y2 and the lines y = 0, y = 2
View SolutionFind the x coordinate of the centre of mass of the bricks shown in figure :

View Solution
