2 mass of block 2 kg & 4 kg are attached to a stiffness spring 100 N/m. 2 kg mass is given velocity 2 m/s & 4 kg to 4 m/s in same direction. Find maximum elongation in the spring during the motion of two blocks.
The correct Answer is:25√3
To solve the problem of finding the maximum elongation in the spring when two blocks are attached to it, we can follow these steps:
Step 1: Determine the Initial Momentum of the System
The total momentum of the system before the blocks interact with the spring can be calculated using the formula:
pinitial=m1⋅v1+m2⋅v2
where:
- m1=2kg (mass of the first block)
- v1=2m/s (velocity of the first block)
- m2=4kg (mass of the second block)
- v2=4m/s (velocity of the second block)
Calculating the momentum:
pinitial=(2kg⋅2m/s)+(4kg⋅4m/s)=4kg m/s+16kg m/s=20kg m/s
Step 2: Calculate the Center of Mass Velocity
The center of mass (CM) velocity Vcm can be calculated using the formula:
Vcm=pinitialm1+m2
Substituting the values:
Vcm=20kg m/s2kg+4kg=20kg m/s6kg≈3.33m/s
Step 3: Determine the Relative Velocities
Next, we find the relative velocities of each block with respect to the center of mass:
- For the 2 kg block:
v1,rel=v1−Vcm=2m/s−3.33m/s=−1.33m/s
- For the 4 kg block:
v2,rel=v2−Vcm=4m/s−3.33m/s=0.67m/s
Step 4: Calculate the Kinetic Energy of Each Block
The kinetic energy of each block can be calculated using:
KE=12mv2
- For the 2 kg block:
KE1=12⋅2kg⋅(−1.33m/s)2=12⋅2⋅1.7689≈1.77J
- For the 4 kg block:
KE2=12⋅4kg⋅(0.67m/s)2=12⋅4⋅0.4489≈0.90J
Step 5: Total Kinetic Energy
The total kinetic energy of the system is:
KEtotal=KE1+KE2≈1.77J+0.90J≈2.67J
Step 6: Relate Kinetic Energy to Spring Potential Energy
At maximum elongation, all kinetic energy will be converted into potential energy stored in the spring:
PEspring=12kx2
where k=100N/m is the spring constant and x is the maximum elongation. Setting the kinetic energy equal to the potential energy:
2.67J=12⋅100N/m⋅x2
Solving for x:
2.67=50x2⟹x2=2.6750⟹x2=0.0534⟹x≈0.231m
Final Answer
The maximum elongation in the spring during the motion of the two blocks is approximately 0.231 m.
---
The total momentum of the system before the blocks interact with the spring can be calculated using the formula:
pinitial=m1⋅v1+m2⋅v2
where:
- m1=2kg (mass of the first block)
- v1=2m/s (velocity of the first block)
- m2=4kg (mass of the second block)
- v2=4m/s (velocity of the second block)
pinitial=(2kg⋅2m/s)+(4kg⋅4m/s)=4kg m/s+16kg m/s=20kg m/s
The center of mass (CM) velocity Vcm can be calculated using the formula:
Vcm=pinitialm1+m2
Substituting the values:
Vcm=20kg m/s2kg+4kg=20kg m/s6kg≈3.33m/s
Next, we find the relative velocities of each block with respect to the center of mass:
- For the 2 kg block:
v1,rel=v1−Vcm=2m/s−3.33m/s=−1.33m/s
- For the 4 kg block:
v2,rel=v2−Vcm=4m/s−3.33m/s=0.67m/s
The kinetic energy of each block can be calculated using:
KE=12mv2
- For the 2 kg block:
KE1=12⋅2kg⋅(−1.33m/s)2=12⋅2⋅1.7689≈1.77J
- For the 4 kg block:
KE2=12⋅4kg⋅(0.67m/s)2=12⋅4⋅0.4489≈0.90J
The total kinetic energy of the system is:
KEtotal=KE1+KE2≈1.77J+0.90J≈2.67J
At maximum elongation, all kinetic energy will be converted into potential energy stored in the spring:
PEspring=12kx2
where k=100N/m is the spring constant and x is the maximum elongation. Setting the kinetic energy equal to the potential energy:
2.67J=12⋅100N/m⋅x2
Solving for x:
2.67=50x2⟹x2=2.6750⟹x2=0.0534⟹x≈0.231m
The maximum elongation in the spring during the motion of the two blocks is approximately 0.231 m.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 3 Level-II
16 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-I
18 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)
28 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions

A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View SolutionTwo bodies of masses 2 kg and 4 kg are moving with velocities 2 m/s and 10 m/s respectively along same direction. Then the velocity of their centre of mass will be
View Solution
Knowledge Check
Two blocks of masses 5kg and 2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are, respectively,
A4m/s,4m/sB10m/s,4m/sC4m/s,10m/sD10m/s,10m/sTwo blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
A110B12√10C12√15D0.15Two block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.
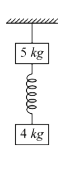 A8m/s2,10m/s2B10m/s2,10m/s2C18m/s2,0D8m/s2,0
A8m/s2,10m/s2B10m/s2,10m/s2C18m/s2,0D8m/s2,0
In figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
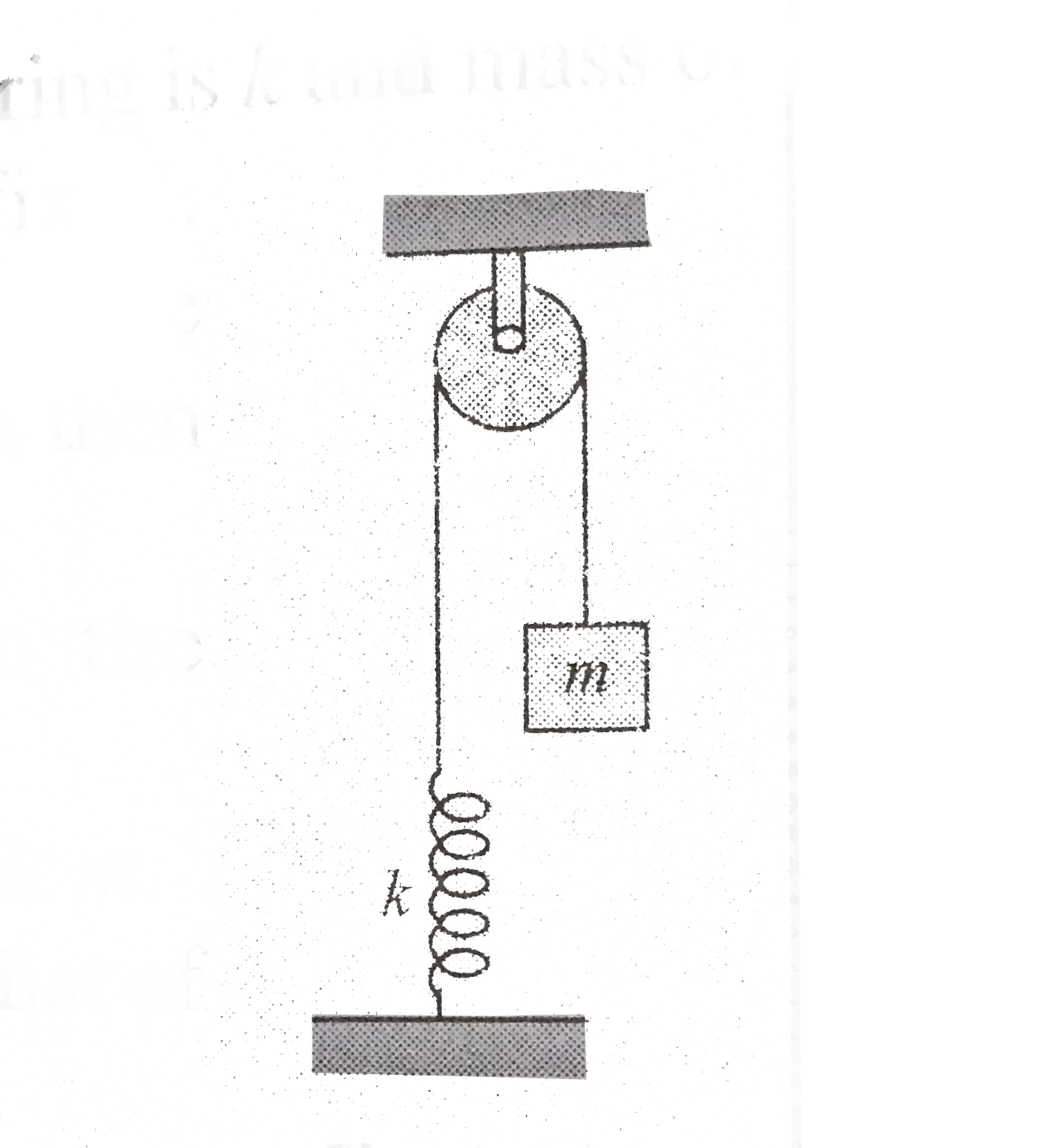
View SolutionForce constant of a spring is 100 N/m. If a 10kg block attached with the spring is at rest, then find extension in the spring.
(g=10m/s2)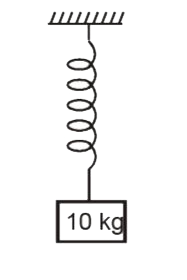
View SolutionTwo blocks A(3kg) and B(6kg) are connected by a spring of stiffness 512 N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. Velocities 1.8m/s and 2.2 m/s are imparted to A and B in opposite direction. The maximum extension in the spring will be –
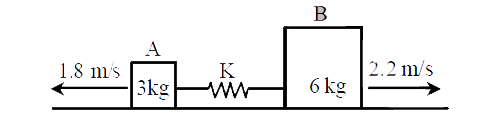
View SolutionA bomb of mass 12 kg explodes into two pieces of masses 4 kg and 8 kg. The velocity of mass 4 kg is 20 m/s. Find the velocity of mass 8 kg.
View SolutionA bomb of mass 12 kg explodes into two piece of masess 4 kg and 8kg . The velocity of mass 4 kg is 20 m/s . Find the velocity of mass 8 kg
View Solution