A ring of diameter 2m oscillates as a compound pendulum about a horizontal axis passing through a point at its rim. It oscillates such that its centre move in a plane which is perpendicular to the plane of the ring. The equibvalent length of the simple pendulum is
2m
4m
1.5 m
3m
The correct Answer is:C
Step by step video, text & image solution for A ring of diameter 2m oscillates as a compound pendulum about a horizontal axis passing through a point at its rim. It oscillates such that its centre move in a plane which is perpendicular to the plane of the ring. The equibvalent length of the simple pendulum is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -2 (Leve-I) ( SECTION - H ) (Combination of two or more SHM)1videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -2 (Leve-I I) ( SECTION - A ) (– Equation of SHM, Velocity and Acceleration in SHM, Energy of SHM)3videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -2 (Leve-I) ( SECTION - E,F ) (Angu lar shm & s imple pendulum)8videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN23videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)14videos
SOUND WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
Radius of gyration of a ring about a transverse axis passing through its centre is
A0.5× diameter of ringBdiameter of ringC2× diameter of ringD(diameter of ring)2 - Question 2 - Select One
A disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
A2π√RgB2π√2RgC2π√2π3gD2π√3R2g - Question 3 - Select One
The moment of inertia of ring about an axis passing through its diameter is I. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
A2IBICI/2DI/4
A ring is suspended at a point on its rim and it behaves as a second's pendulum when it oscillates such that its centre move in its own plane. The radius of the ring would be (g = π2)
View SolutionAn annular ring of internal and outer radii r and R respectively oscillates in a vertical plane about a horizontal axis perpendicular to its plane and passing through a point on its outer edge. Calculate its time period and show that the length of an equivalent simple pendulum is 3R2 as r→0 and 2R as r→R.
View SolutionA ring-1 oscillate with period T1 about tangential axis in the plane of ring and an another ring-2 oscillate with period T2 about tangential axis tangential axis perpendicular to plane of ring T1T2?
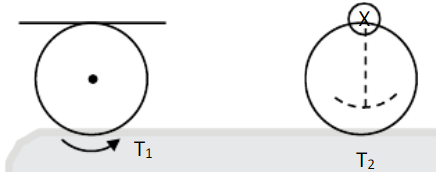 View Solution
View SolutionA ring is suspended at a point on its rim and it behaves as a second’s pendulum when it oscillates such that its centre move in its own plane. The radius of the ring would be (g = π2)
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View Solution

