A highly conducting solid cylinder of radius a and length l is surrounded by a co-axial layer of a material having thermal conductivity K and negligible heat capacity. Temperature of surrounding space (out side the layer) is T0, which is higher than temperature of the cylinder. If heat capacity per unit volume of cylinder material is s and outer radius of the layer is b, calculate time required to increase temperature of the cylinder from T1→T2. Assume end faces to be thermally insulated.
Step by step video & image solution for A highly conducting solid cylinder of radius a and length l is surrounded by a co-axial layer of a material having thermal conductivity K and negligible heat capacity. Temperature of surrounding space (out side the layer) is T_0, which is higher than temperature of the cylinder. If heat capacity per unit volume of cylinder material is s and outer radius of the layer is b, calculate time required to increase temperature of the cylinder from T_1 to T_2. Assume end faces to be thermally insulated. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEAT - 1BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - I) Previous Year | JEE Main
10 Videos
- HEAT - 1BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced
22 Videos
- HEAT - 1BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -3 (Level - I) Subjective | JEE Advanced
20 Videos
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 Section - B Previous Years Problems
15 Videos
- HEAT TRANSFER & THERMAL EXPANSION BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - Exercise - 3 Section-B
19 Videos
Similar Questions
A rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
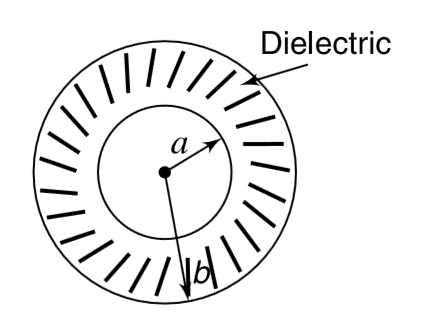
View SolutionFind the capacitance of an isolated spherical conductor of radius a surrounded by a concentric layer of dielectric of outer radius b and relative permittivity. ε
View Solution
Knowledge Check
The radius and height of a cylinder are equal. If the radius of the sphere is equal to the height of the cylinder, then the ratio of the rates of increase of the volume of the sphere and the volume of the cylinder, is
A4:3B3:4C4:3πD3π:4A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylinderical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effictive thermal conductivity of the system is
AK1+K2BK1K2/(K1+K2)C(K1+3K2)/4D(3K1+3K2)/4
A long charged cylinder of linear charged density à is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View SolutionA cylinder of radius R, made up of a material (thermal conductivity k1) is surrounded by a cylindrical sheet of inner radius R and outer radius 2R (thermal conductivity k2). The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Calculate the effective thermal conductivity of the system.
View SolutionA long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cyclinder. What is the electric field in the space between the two cylinders ?
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by cylindrical shell of inner radius R and outer radius 2R made of a material of thermal con-ductivity K2 The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionConducting ball of radius a is surrounded by a layer of dielectric having inner radius a and outer radius b. The dielectric constant is K. The conducting ball is given a charge Q. Write the magnitude of electric field and electric potential at the outer surface of the dielectric.
View SolutionThe material of a solid cone is converted into the shape of a solid cylinder of equal radius. If the height of the cylinders 5 cm, what is the height of the cone ?
View Solution
