In a YDSE, D = 1m, d = 1mm and λ=1/2mm
Find the no of maxima and minima obtained on the screen.
To solve the problem of finding the number of maxima and minima in a Young's Double Slit Experiment (YDSE), we will follow these steps:
Step 1: Understand the Given Data
- Distance between the slits (d) = 1 mm = 1 x 10^-3 m
- Distance from the slits to the screen (D) = 1 m
- Wavelength of light (λ) = 1/2 mm = 0.5 mm = 0.5 x 10^-3 m
Step 2: Calculate the Maximum Order of Maxima (n_max)
The formula to find the maximum order of maxima is given by:
nmax=dλ
Substituting the values:
nmax=1×10−30.5×10−3=2
This means the highest order of maxima that can be observed is 2.
Step 3: Calculate the Maximum Order of Minima (n_min)
The formula to find the maximum order of minima is given by:
nmin=dλ+12
Substituting the values:
nmin=1×10−30.5×10−3+12=2+0.5=2.5
Since we can only have whole orders of minima, we take the integer part:
nmin=2
Step 4: Calculate Total Number of Maxima
The total number of maxima includes the central maximum and the maxima on both sides:
Total Maxima=2×nmax+1
Total Maxima=2×2+1=4+1=5
Step 5: Calculate Total Number of Minima
The total number of minima includes the minima on both sides:
Total Minima=2×nmin
Total Minima=2×2=4
Final Results
- Total number of maxima = 5
- Total number of minima = 4
- Distance between the slits (d) = 1 mm = 1 x 10^-3 m
- Distance from the slits to the screen (D) = 1 m
- Wavelength of light (λ) = 1/2 mm = 0.5 mm = 0.5 x 10^-3 m
The formula to find the maximum order of maxima is given by:
nmax=dλ
nmax=1×10−30.5×10−3=2
The formula to find the maximum order of minima is given by:
nmin=dλ+12
nmin=1×10−30.5×10−3+12=2+0.5=2.5
nmin=2
The total number of maxima includes the central maximum and the maxima on both sides:
Total Maxima=2×nmax+1
Total Maxima=2×2+1=4+1=5
The total number of minima includes the minima on both sides:
Total Minima=2×nmin
Total Minima=2×2=4
- Total number of maxima = 5
- Total number of minima = 4
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 1 (Objective Problems | JEE Main) Section A - Interference Problems + Wavefronts & Hugens Principle9videos
WAVE OPTICS
- BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 1 (Objective Problems | JEE Main) Section B - YDSE Experiment8videos
WAVE OPTICS
- BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)7videos
WAVE MOTION
- BOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)10videos
WAVES
Similar Questions
In a YDSE, D = 1m, d = 1mm and λ=1/2mm
Find a distance between the first and central maxima on the screen.View SolutionIn a YDSE, D=1M,d=1mm,andλ=1/2mm.
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.View Solution
Knowledge Check
- Question 1 - Select One
In YDSE, D=1m,d=1mm, and λ=5000nm. The distance of the 100th maxima from the central maxima is
A12mB√32 mC1√3 mDdoes not exist - Question 2 - Select One or More
In YDSE,D=1m,d=4mm and λ=12mm in the figure shown, a parallel beam of light is incident on the plane of the slits of YDSE. Light incident on the slit s1, passes through a medium of variable refractive index μ=(2x+1) (where x is the distance from the plane of slits in mm) up to a distance l=1mm before falling on s1. Rest of the space filled with air. Then choose the correct option (s):
 APosition of central brigh fringe is at a distanc y=1√3m above the central lineBPosition of central bright fringe is at a distance y=12m above the central lineCNumber of maxima obtaining on the screening is 7DNumber of maxima obtaining on the screening is 8
APosition of central brigh fringe is at a distanc y=1√3m above the central lineBPosition of central bright fringe is at a distance y=12m above the central lineCNumber of maxima obtaining on the screening is 7DNumber of maxima obtaining on the screening is 8 - Question 3 - Select One
In YDSE, D=2mm,D=2m, and λ=500nm. If intensities of two slits are I0 and 9I0, then find intensity at y=16mm.
A7I0B10I0C16I0D4I0
In the YDSE apparatus shown in figure, d<<D and d=6λ. Find

(a) total number of maximas and minimas on the screen .
(b) two y-coordinates corresponding to third order maxima.View SolutionA beam of light consisting of wavelengths 6000 Å and 4500 Å is used in a YDSE with D = 1 m and d = 1 mm. Find the least distance from the central maxima, where bright fringes due to the two wavelengths coincide.
View SolutionIn the set up shown in figure dltltD and d=4lambda, find.
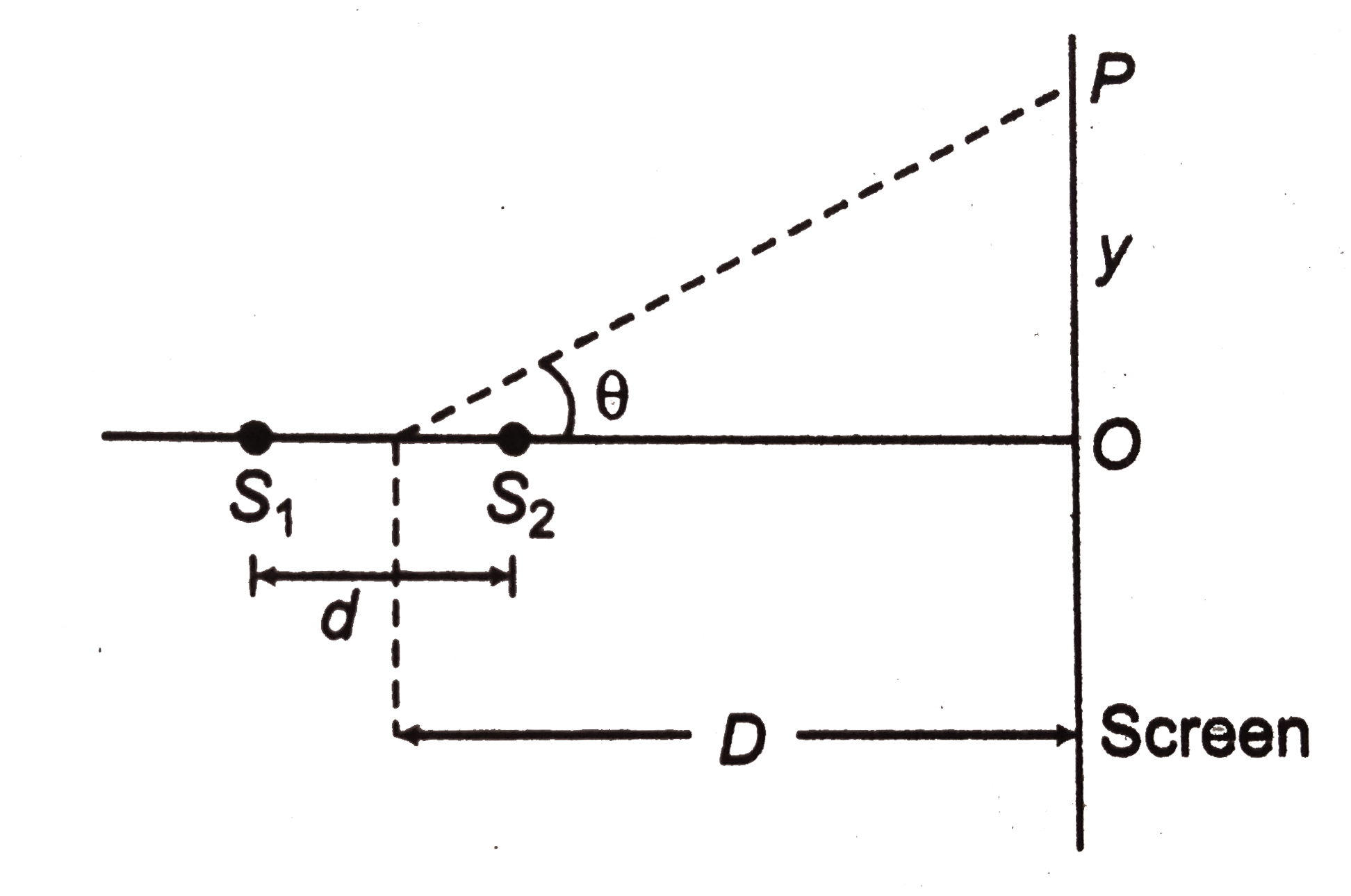
(a) total number of maximas and minimas on the screen
(b) y-coordinates corresponding to minima nearest to O.View SolutionIn YDSE a=2mm, D = 2m, λ=500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionIn a YDSE experiment, d = 1mm, λ= 6000Å and D= 1m. The minimum distance between two points on screen having 75% intensity of the maximum intensity will be
View Solution

