A Young's double slit interference arrangement with slits S1 and S2 is immersed in water (refractive index =4/3) as shown in the figure. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........

The correct Answer is:3
Step by step video & image solution for A Young's double slit interference arrangement with slits S_(1) and S_(2) is immersed in water (refractive index =4//3) as shown in the figure. The positions of maxima on the surface of water are given by x^(2) = p^(2)m^(2)lambda^(2)-d^(2), where lambda is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is .......... by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 4 (Level - I) Previous Year | JEE Main20videos
WAVE OPTICS
- BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)7videos
WAVE MOTION
- BOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)10videos
WAVES
Similar Questions
When an unpolarized light of intensity I0 is incident on a polarizing sheet, the intensity of the light which does not get transmitted is
01:53View SolutionA string is stretched between fixed points separated by 75.0cm. It is observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. Then, the lowest resonant frequency for this string is
10:46View SolutionA transverse harmonic disturbance is produced in a string. The maximum transverse velocity is 3m/s and maximum transverse acceleration is 90m/s. If the wave velocity is 20m/s then find the waveform.
02:02View SolutionDetermine what happens to the double slits interference pattern if one of the slits is covered with a thin, transparent film whose thickness is lambda/(2(mu-1)) , where lambda is the wavelength of the incident light and mu is the index of refraction of the film.
02:46View SolutionIn figure S is a monochromatic source of light emitting light of wavelength of wavelength lambda (in air). Light on slits S_(1) from S and then reaches in the slit S_(2) and S_(3) through a medium of refractive index mu_(1) . Light from slit S_(2) and S_(3) reaches the screen through a medium of refractive index mu_(3) . A thin transparent film of refractive index mu_(2) and thickness t is used placed in front of S_(2) . Point P is symmetrical w.r.t. S_(2) and S_(3) . Using the values d = 1 mm, D = 1 m, mu_(1) = 4//3 , mu_(2) = 3//2, mu_(3) = 9//5 , and t = (4)/(9) xx 10^(-5) m , a. find distance of central maxima from P, b. If the film in front of S_(2) is removed, then by what distance and in which direction will be central maxima shift ? .
07:39View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
02:42View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be (assume θ to be a small angle)
01:47View SolutionA Young's double slit interference arrangement with slits S_(1) and S_(2) is immersed in water (refractive index =4//3 ) as shown in the figure. The positions of maxima on the surface of water are given by x^(2) = p^(2)m^(2)lambda^(2)-d^(2) , where lambda is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........
View SolutionIn Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,where I0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)
 View Solution
View SolutionIn a Young's double slit experiment, let S_(1) and S_(2) be the two slits, and C be the centre of the screen. If angle S_(1)CS_(2)=theta and lambda is the wavelength, the fringe width will be
View SolutionA Young's double-slit interference arrangement with slits S_1 and S_2 is immersed in water (refractive index = 4/3) as shown in the figure. The positions of maxima on the surface of water are given by x^2 = p^2m^2lambda^2 - d^2 , where lambda is the wavelength of light in air (refractive index = 1), 2d is the separation between the slits and m is an interger. The value of p is {:(0,1,2,3,4,5,6,7,8,9):}
View SolutionConsider the arrangement shown in figure, By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of S1S2 and S3S4. When z=Dλ2d, the intensity measured at P is I. Find this intensity when z is equal to 1) Dλd, (2) 3Dλ2d and (3) 2Dλd.
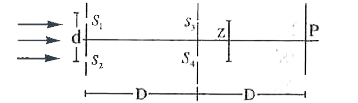 05:19View Solution
05:19View SolutionLight of wavelength lambda = 500 nm falls on two narrow slits placed a distance d = 50 xx 10^(-4) cm apart, at an angle phi = 30^(@) relative to the slits shown in figure. In front of the lower slit, a slab of thickness 0.1 mmand refractive index 3/2 is placed. The interference pattern is observed on a screen at a distance D = 2m from the slits S_(1)O = S_(2)O = d//2 The position of central maxima is at an angular position 'theta' with line OB
03:17View SolutionIn Young's double slit experiment the point source is placed slightly off the central axis as shown in figure. The plane of slits (S1,S2) and screen are separated by a distance of 2m. The separation between the slits is 10 mm. The position of the slit above the axis is 1mm. if the wavelength λ=4000Å in the above arrangement

If central maximum is to occur at point 'P' then a sheet of thin film of refractive index μ=1.5 can be introduced in the path of rays from one the slits to the point 'P'. (t-thickness of film)03:39View SolutionIn Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,whereI0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)
 01:48View Solution
01:48View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
09:32View Solution

