Find the minimum value of x for which a maxima is obtained at P.
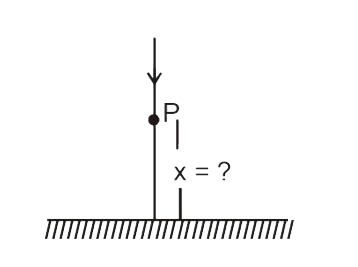
Video Solution
Text Solution
For maxima, Δx=λ (because x should be minimum) Path difference between the direct & reflected ray
=x+λ2+x
(due to reflection, a phase change of π or path change of λ2 takes place)
∴λ=x+λ2+x
2x=λ2
⇒x=λ4
|
Topper's Solved these Questions
- WAVE OPTICS BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 1 (Objective Problems | JEE Main) Section A - Interference Problems + Wavefronts & Hugens Principle
9 Videos
- WAVE OPTICS BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 1 (Objective Problems | JEE Main) Section B - YDSE Experiment
8 Videos
- WAVE MOTION BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)
7 Videos
- WAVESBOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)
10 Videos
Similar Questions
Find the value of θ for which a maxima is obtained at P.

View SolutionThe interference pattern is observed at P due to superimposition of two rays coming out from a source S as shown in the figure . The value of l for which maxima is obtained at P is (R is a perfect reflecting surface) : -

View Solution
Knowledge Check
Find the minimum value of sin2x
A-1B0C1D1/2Interference pattern is observed at 'P' due to superimposition of two rays coming out from a source 'S' as shown in the figure. The value of '1' for which maxima is obtained at 'P' is : (R is perfect reflecting surface)
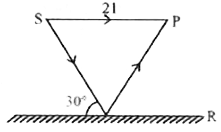 A1=2nλ√3−1B1=(2n−)λ2(√3−1)C1=(2n−)λ√34(2−√3)D1=(2n−)λ√3−1
A1=2nλ√3−1B1=(2n−)λ2(√3−1)C1=(2n−)λ√34(2−√3)D1=(2n−)λ√3−1Find the minimum value of |x−3|+11
A8B11C0D−8
Find the minimum value of sin x + cos x.
View SolutionFind minimum value of (9−x)(2−x)
View SolutionFind the minimum value of the function xx.
View SolutionFind the minimum value of the following and find the value of x for which the expression takes the minimum value :
16x2−24x−26
View SolutionFind the minimum value of the following and find the value of x for which the expression takes the minimum value :
9x2−8x−8
View Solution
