Light of wavelength 520nm passing through a double slit,produced interference pattern of relative intensity versus deflection angle θ as shown in the figure.find the separation of between the slits.
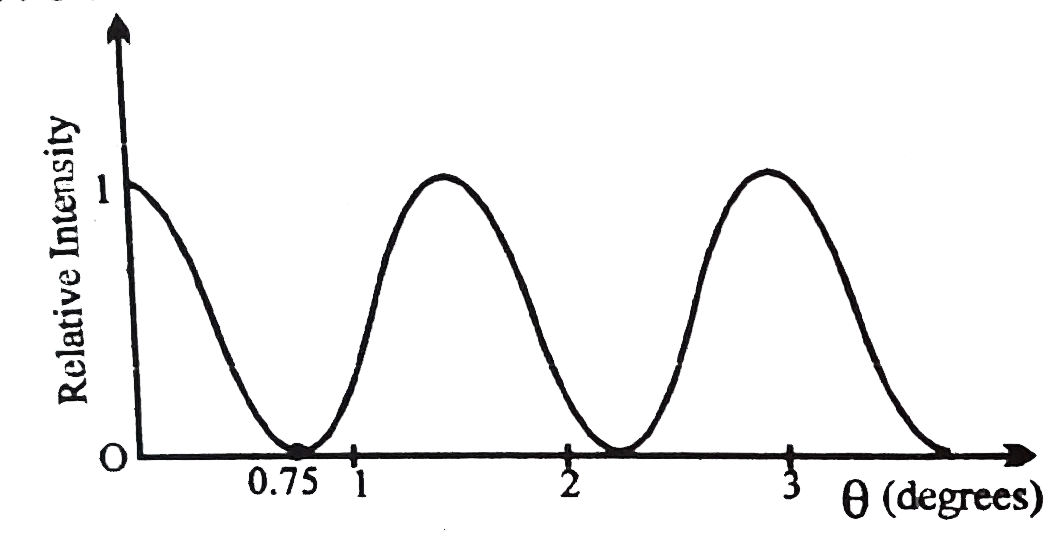
The correct Answer is:1.98×10−2mm
Step by step video & image solution for Light of wavelength 520nm passing through a double slit,produced interference pattern of relative intensity versus deflection angle theta as shown in the figure.find the separation of between the slits. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE OPTICS BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 3 (Level - II) (Subjective | JEE Advanced) Section A - Interference Problems + Wavefronts & Hugen’s Principle
4 Videos
- WAVE OPTICS BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 3 (Level - II) (Subjective | JEE Advanced) Section B - YDSE Experiment
5 Videos
- WAVE OPTICS BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 3 (Level - I) (Subjective | JEE Advanced) Section A - Interference Problems + Wavefronts & Hugen’s Principle
6 Videos
- WAVE MOTION BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)
7 Videos
- WAVESBOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)
10 Videos
Similar Questions
In young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
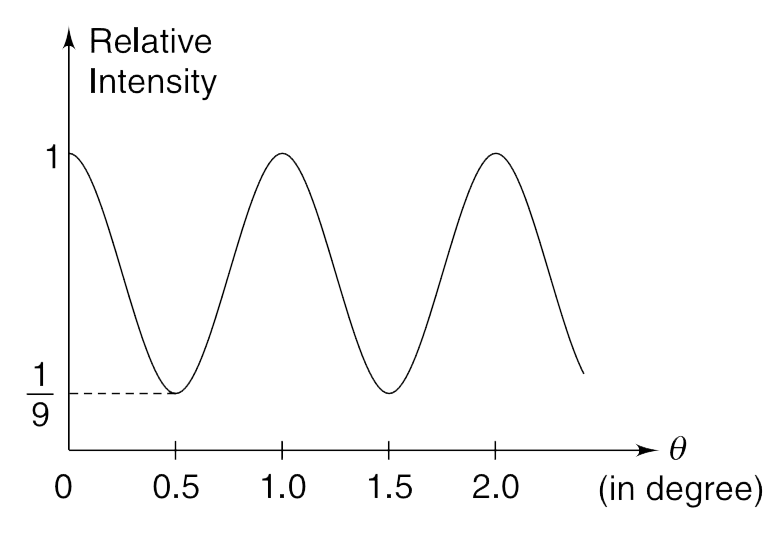
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
View SolutionLight of wavelength 620 nm passes through a double slit, yielding a diffraction pattern whose graph of intensity l versus angular position θ is shown in Figure. Calculate (a) the slit width and (b) the slit separation. (c) Verify the displayed intensities of thc m = 1 and m = 2 interference fringes.
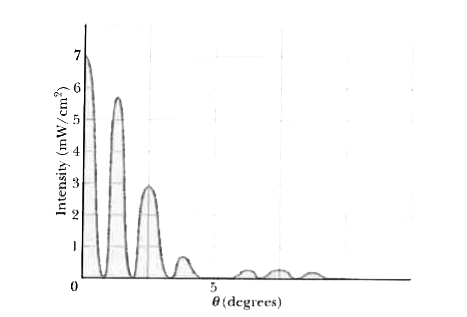
View Solution
Knowledge Check
In a double slit interference pattern, the first maxima for infrared light would be
Aat the same place as the first maxima for green lightBcloser to the centre than the first maxima for green lightCfarther from the centre than the first maxima for green lightDinfrared light does not produce an interference patternIn a double-slit interference pattern, the first maxima for infrared light would be
AAt the same place as the first maxima for green lightBCloser to the center than the first maxima for green lightCFarther from the center than the first maxima for green lightDInfrared light does not produce an interference pattern
Suppose a monochromatic X-ray beam of wavelength 100 pm is sent through a Young's double slit and the interference pattern is observed on a photographic plate placed 40 cm away from the slit. What should be the separation between the slits so that the successive maxima on the screen are separated by a distance of 0*1 mm?
View SolutionLaser light of wavelength 630nm incident on a pair of slits produces an interference pattern where bright fringes are separated by 8.1mm. Another light produces the interference pattern, where the bright fringes are separated by 7.2mm. Calculate the wavelength of second light.
View SolutionIn Young's double slit experiment the interference pattern is found to have an intensity ratio between bright and dark fringes as 9. This implies
View SolutionA source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
View SolutionLaser light of wavelength 630 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 8.1 mm. A second laser light produces an interference pattern in which the fringes are separated by 7.2 mm. Calculate the wavelength of the second light.
View SolutionLaser light of wave length 600 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 8mm. A second light produces an interference pattern in which the fringes are separated by 12 mm. Calculate the wavelength of the second light.
View Solution
