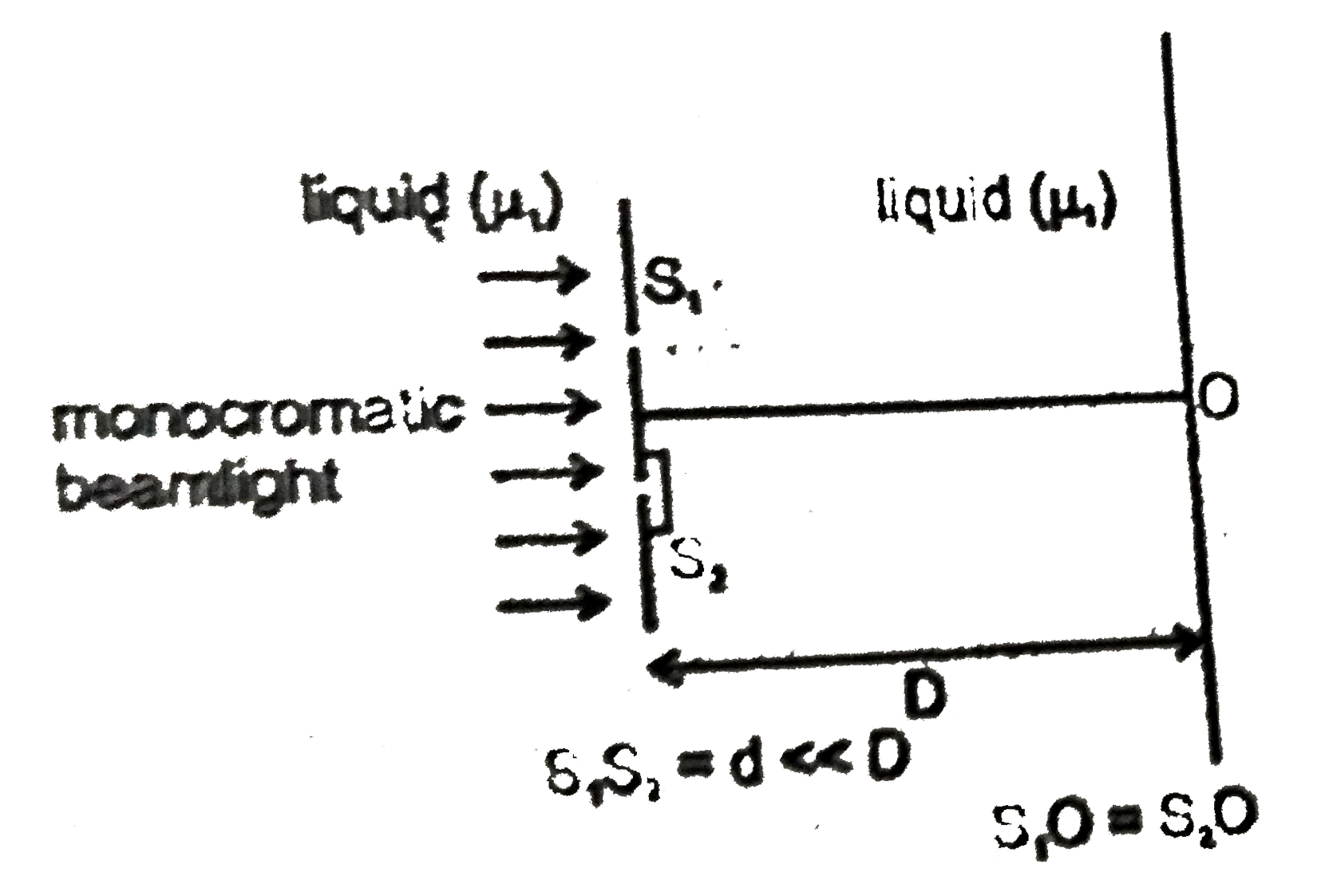
A Young's double-slit interference arrangement with slits $S_{1} and S_{2}$ is immersed in water (refractive index = 4/3) as shown in the figure. The positions of maxima on the surface of water are given by $x^{2} = p^{2} m^{2} λ^{2} - d^{2}$ , where $λ$ is the wavelength of light in air (refractive index = 1), 2d is the separation between the slits and m is an interger. The value of p is
$A Young's double-slit interference arrangement with slits S1 and S2 is immersed in water (refractive index = 4/3) as shown in the figure. The positions of maxima on the surface of water are given by x^2 = p^2m^2lambda^2 - d^2, where lambda is the wavelength of light in air (refractive index = 1), 2d is the separation between the slits and m is an interger. The value of p is {:(0,1,2,3,4,5,6,7,8,9):}$
$\begin{matrix} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \end{matrix}$

Text Solution

Verified by Experts

The correct Answer is:3

Updated on:21/07/2023

In a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec $μ$ is placed in front of the slit $S_{1}$ , then the path difference $(S_{1} P - S_{2} P)$ is

A(a) Decreases by $(μ - 1) t$
B(b) Increases by $(μ - 1) t$
C(c) Does not change
D(d) Increases by $μ t$
In young's double slit experiment, distance between the slit $S_{1} and S_{2}$ is d and the distance between slit and screen is D . Then longest wavelength that will be missing on the screen in front of $S_{1}$ is
A $\frac{d^{2}}{D}$
B $\frac{d^{2}}{2 D}$
C $\frac{D}{d^{2}}$
DNone of these