As shown in Fig. the two sides of a step ladder BA and CA are 1.6m long and hinged at A. A rope DE,0.5m is tied half way up. A weight 40kg is suspended from a point F,1.2m from B along the ladderBA. Assuming the floor to be fricionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g=9.8m/s2)
(Hint. Consider the eqilibrium of each side of the ladder separately.)
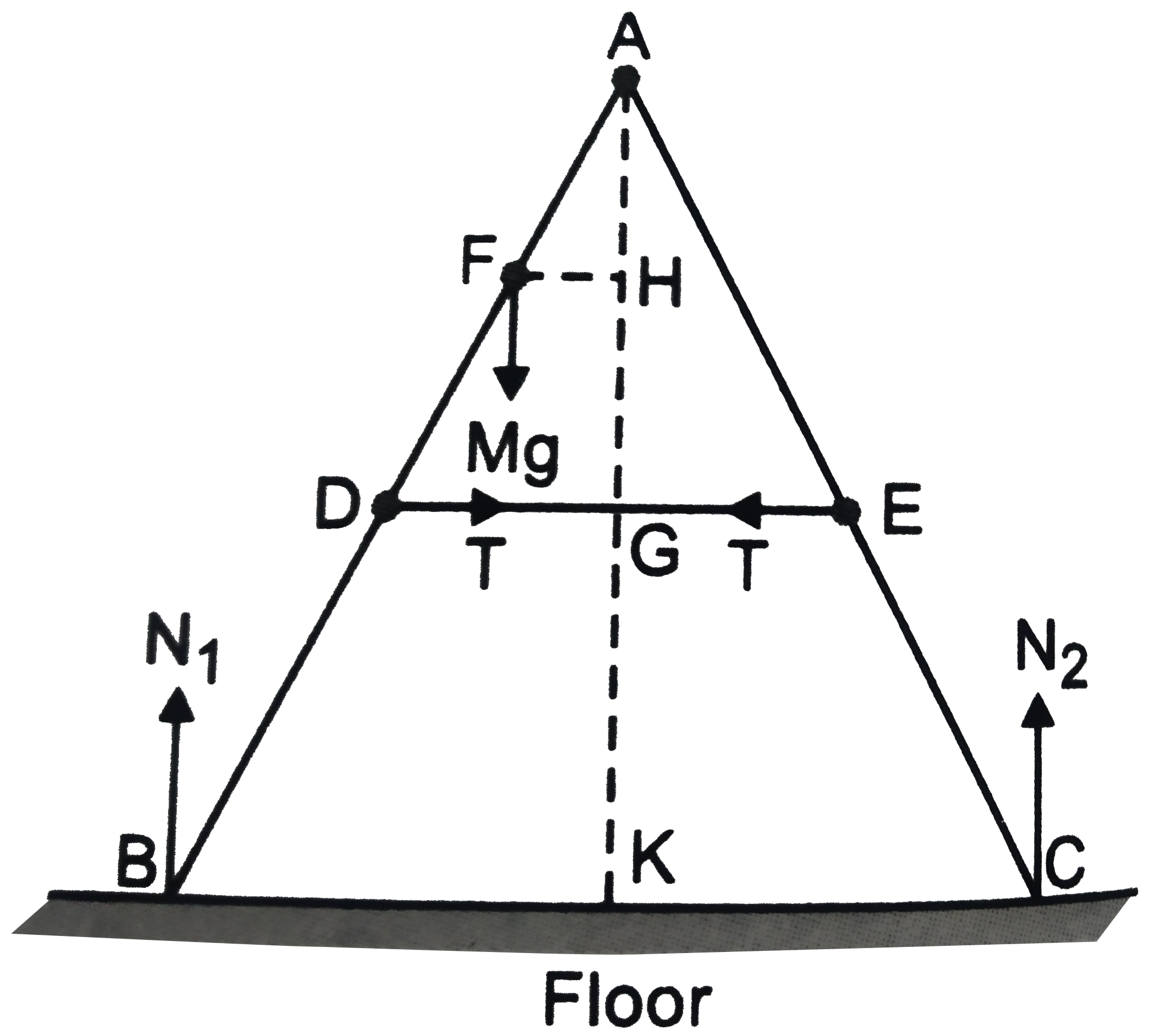
The forces acting on the ladder are shown in Fig. 7.14. Here, IV=40kg=40×9.8N=392N,AB=AC=1.6m,BD=1/2×1.6m=0.8m,BF=1.2m andDE0.5m
In the Fig. ΔADE and ΔABC are similar triangles, hence
BC=De×ABAD=0.5×1.60.8=1.0m
Now, considering equilibrium at point B ∑τ=0
∴ W×(MB)=NC×(CB)
But MB=KB×BFBA=0.5×1.21.6=0.375m
Substituting this value in (i), we get
∴ NC=W×(MB)(CB)=392×0.3751=147N
Again considering equilibrium at point C in similar manner, we have
W×(MC)=NB×(BC)
∴ NB=W×(MC)(BC)=W×(BC−BM)(BC),
(392×(1−0.375))/1=245N
Now, it can be easily shown that tension in the string T=NB−NC=245−147=98N.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE33videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NCERTCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE16videos
PHYSICAL WORLD
- BOOK - NCERTCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE22videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The step-ladder shown in figure 6.11 is 8 m long and hinged at C.BD is a tie rod 2.5 m long half way up. A man of 86 kg climbs 6 m along the ladder . Find the tension in the tie rod the forces exerted on the ladder by the assuming the floor to frictionless and the ladder weightless.

[Hints: Consider the free-body diagram of the sides of the ladder.]View SolutionA 3m along ladder weighing 20kg leans on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the rection forces of the wall and the floor.
View SolutionA weight of mass m is suspended from a hinged bracket (Fig.).
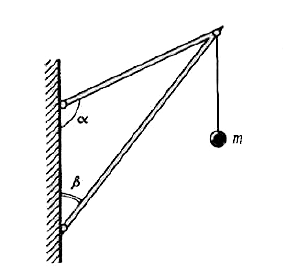
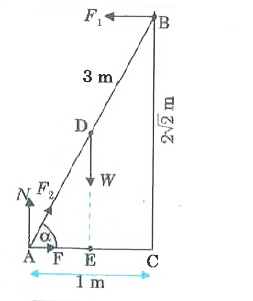
Find the forces in the rods making up the bracket.View SolutionA 3 m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in the following figure, Find the reaction forces of the wall and the floor.
 View Solution
View SolutionA ladder leaning against a wall makes an angle of 60o with the ground. If the length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.
View SolutionA bucket is suspended by two light ropes a and b as shown in fig. 2E.3 (a). Determine the tensions in the ropes a and b.
 View Solution
View SolutionA 15-m long ladder is placed against a wall to reach a window 12 m high.Find the distance of the ladder from the wall.
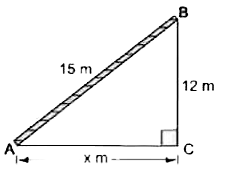 View Solution
View SolutionA ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
View SolutionA 5.5m long ladder is leaned against a wall. The ladder reaches the wall to a height of 4.4m. Find the distance between the wall and the foot of the ladder.
View SolutionA ladder of length 50 m rests against a vertical wall, at a height of 30 m from the ground. Find the inclination of the ladder with the horizontal. Also find the distance between the foot of the ladder and the wall.
View Solution

