Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show P=Pi+miV
where pi is the momentum of the ith particle (of mass mi) and pi=mivt Notevi is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass ∑pt=0
(b) Show K=K'+1/2MV2
where K is the total kinetic energy of the system of particles. K' is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show L=L'+R×MV
where L'=∑r't×p't is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember r'i=ri−R, rest of the notation is the standard notation used in the chapter. Note L' and MR×V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show dL'dt=∑r'i×dp'dt
Further, show that
dL'dt=τ'ext
where τext is the sum of all external torques acting on the system about the centre of mass.
(Hint : Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Here →ri=→r'i+→R+R and →Vi=→V'i+→V
where →r'i and →v'i denote the radius vector and velocity of the ith particle referred to centre of mass O as the new origin and →V is the velocity of centre of mass relative to O.
(a)Momentum of ith particle
→P=mi→V'i
=mi(→V'i+→V)(since→Vi=→V'i+→V)
or →P=mi→V'i+mi→V
→P=→Pi+mi→V
(b) KInetic energy of the system of particles.
K=12∑miV2i
=12∑mi→Vi.→Vi
=12∑mi(→V'i+→V)(→V'i+→V)
=12∑mi(V'2i+V2+2→V'i.→V)
=12∑miV2i+12∑miV'2i+∑mi→Vi.→V
=12MV2+K'
where M=∑mi
= total mass of the system
K'=12∑imiV'2i
=kinetic energy of motion about the centre of mass
or 12Mv2= kinetic energy of motion of centre of mass. (Proved)
since ∑imi→Vi.→V=∑mid→ridt.→V
=ddt(∑mi→r'i).→V=ddt(M→R.→V)
(c ) Total angular momentum of the system of particles.
→L=→ri×→p
=(→ri+→R)×∑imi→Vi
=(→r'i+→R)×∑imi(→V'i+→V)
∑i(→R×mi→V)+∑i→r'i×mi→V'i+(∑imi→ri)
×→V+→R×∑imi→Vi
=∑i(→R×mi→V)+∑i→r'i×mi→–––(i)+(∑imi→r'i)
×→V+→R×ddt(∑imi→r'i)
The last two terms vanish for both contain the factor ∑mi→r'i which is equal to
∑imi→ri=∑imi(→r'i−→R)=M→R−M→R=→0
from the definition of centre of mass. Also
∑i(→R×mi→V)=→R×M→V
so that →L=→R×M→V+∑ir'i×→Pi
or →L=→R×M→V+→L'
(d). where From previous solution
→L'=∑→ri'×d→Pidt=∑d→ri'dt×→Pi
=∑→ri'×d→Pidt
=∑→ri×→Fexti=→τext'
since ∑d→ri'dt×→Pi=∑d→ri'dt×m→vi×m→vi=0
total torque →τ=∑→ri×→Fexti
=∑(→ri+→R)×→Fexti
=∑(→ri+→R)×→Fexti
=∑→ri'×→Fexti+→R×Sium→Fexti
=→τext'+→τext0
where →τext is the total torque about the centre of mass as origin and →τext0 that about the origin O.
→τext'=∑→ri'×→Fexti
=∑→ri×d→Pi'dt=ddt∑i(→ri×→Pi)=d→L'dt.
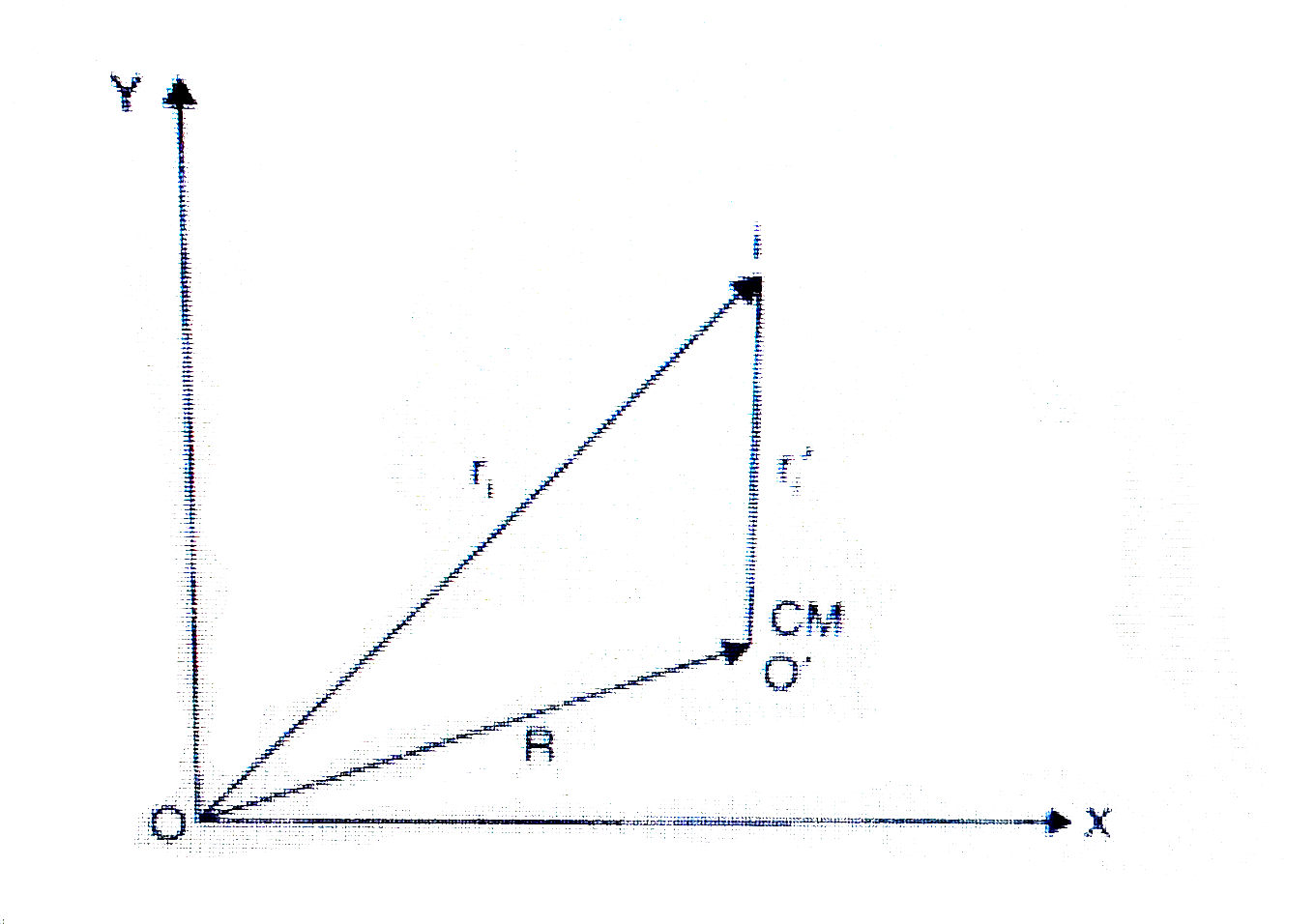
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERTCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERTCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERTCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
Separation of motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(a)n Show →p=→pi+mi→V where →pi is the momentum of the ith particle (of mass mi) and →pi=mi→vi, Not →vi is the velocity of the ith particle relative to the centre ofmass.
Also, prove using the definition of the centre of mass ∑→pi=0
(b) Show K=K'+1/2MV2 where K is the total kinetic energy of the system of particles, K is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system)
(c) Show →L=→L+→R×MV
where →L'=∑→ri×→pi is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember →ri=→ri−→R, reat of the notation is the standard notation used in the chapter. Note →L'andM→R×→V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show d→Ldt=∑→ri×d→p'dt Further show that d→L'dt=→τext' where Text is the sum of all external torques acting on the system about the centre of mass. (Hint: Use the definition of centre of mass and Newton's Third Law. Assume the internal forces between any two particles aet along the line joining the particles.)
View SolutionThe rate of change of angular momentum of a system of particles about the centre of mass is equal to the sum of external torque about the centre of mass when the centre of mass is :
View Solution
Knowledge Check
The rate of change of angular momentum of a system of particles about the centre of mass is equal to the sum of external torque about the centre of mass when the centre of mass is :
AFixed with respect to an inertial frame.Bin linear acceleration.Cin rotational motion.Dis in a translational motion.The motion of the centre of mass of a system of two particles is unaffected by their internal forces.
Airrespective of the actual direction of the internal forces.Bonly if they are along the line joining the particlesConly if they are at right angles to the joining the particlesDonly if they are obliquely inclined to the line joining the particle.Considering a body of mass m, radius R rotating with angular speed ω about the centre of the mass and with a velocity v of centre of mass, the most appropriate definition of rolling motion will be
Av = R ωBthe point of contact is stationaryCthe point of contact is stationary with respect to the surfaceDthe body purely rotates about the point of contact
Linear Momentum Of Two System Of Particle Relative To Centre Of Mass Frame
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionThe velocities of two particles of masses m1 and m2 relative to an observer in an inertial frame are v1 and v2. Determine the velocity of the center of mass relative to the observer and the velocity of each particle relative to the center of mass.
View SolutionConsidering a body of mass m, radius R rotating with angular speed ω about the centre of the mass and with a velocity v of centre of mass, the most appropriate definition of rolling motion will be
View Solution
