In a cylindrical vessel containing liquid of density ρ there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be

h2−h1
h2+h1
h2−h12
h2+h12
The correct Answer is:A
Step by step video & image solution for In a cylindrical vessel containing liquid of density rho there are two holes in the side walls at heights of h_(1) and h_(2) respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE-2 (ASSERTION AND REASON)
28 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE-3 SECTION-A (PREVIOUS YEAR PROBLEM)
61 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - QUESTIONS FOR PRACTICE
6 Videos
- HEAT-2 BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-4 (LEVEL-II)
30 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 2)
6 Videos
Similar Questions
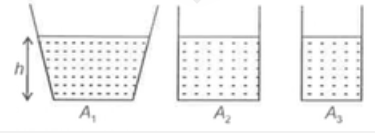
Three vessels containing same liquid, upto the same height h, then pressure at the bottom is (A1>A2>A3)
View SolutionA cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
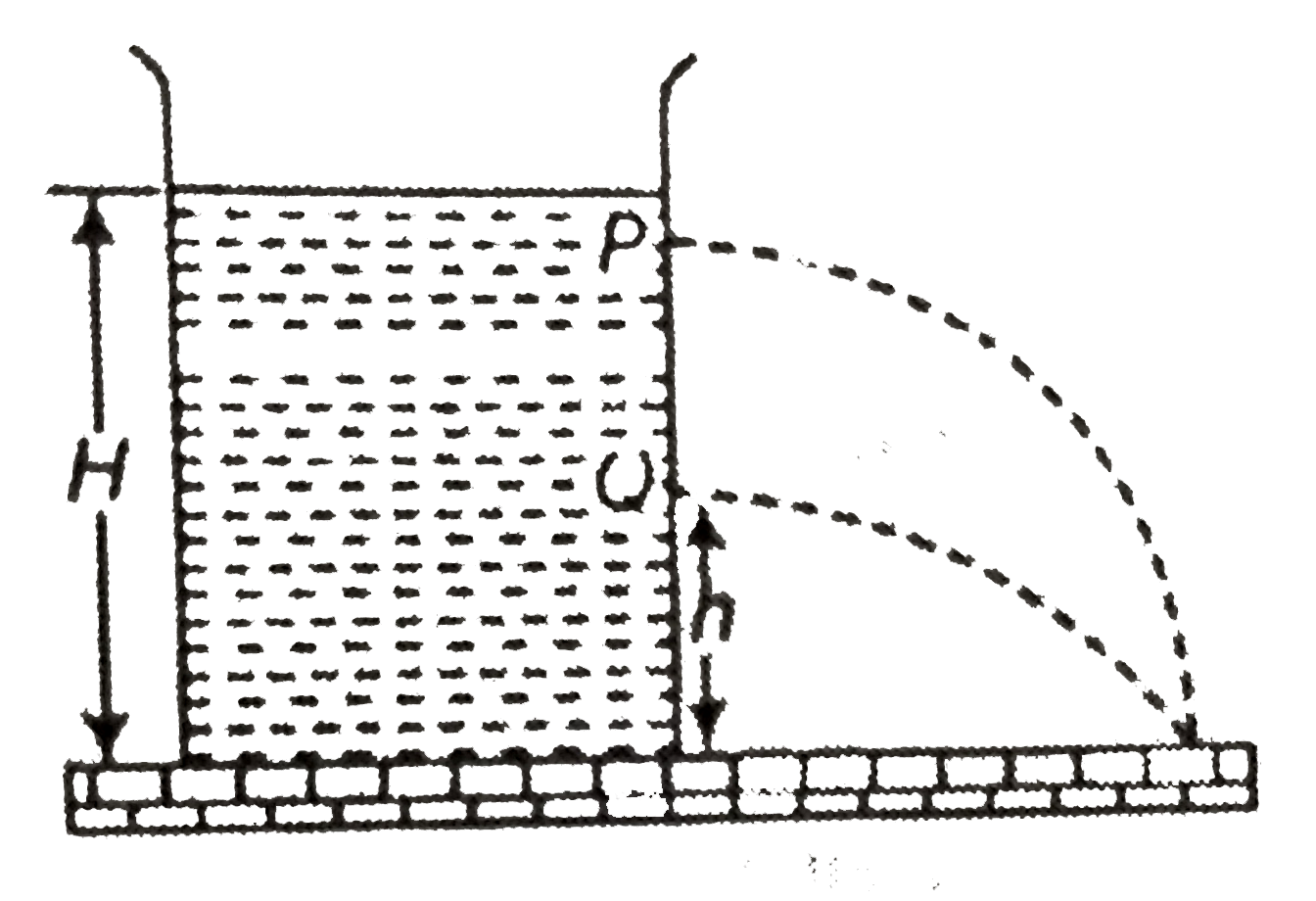
View Solution
Knowledge Check
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA)
A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA)A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgA
A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgAIf a vessel containing a fluid of density ρ upto height h is accelerated vertically downwards with accelerations a0. Then the pressure by fluid at the bottom of a vessel is
Ap=p0+ρgh+ρha0Bp=p0+ρghCp=p0+ρh(g−a0)Dp=p0ρgh
Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View SolutionAn open vessel containing the liquid upto a height of 15 m. A small hole is made at height of 10 m from the base of the vessel then the initial velocity of efflux is (g = 10 m/s2)
View Solution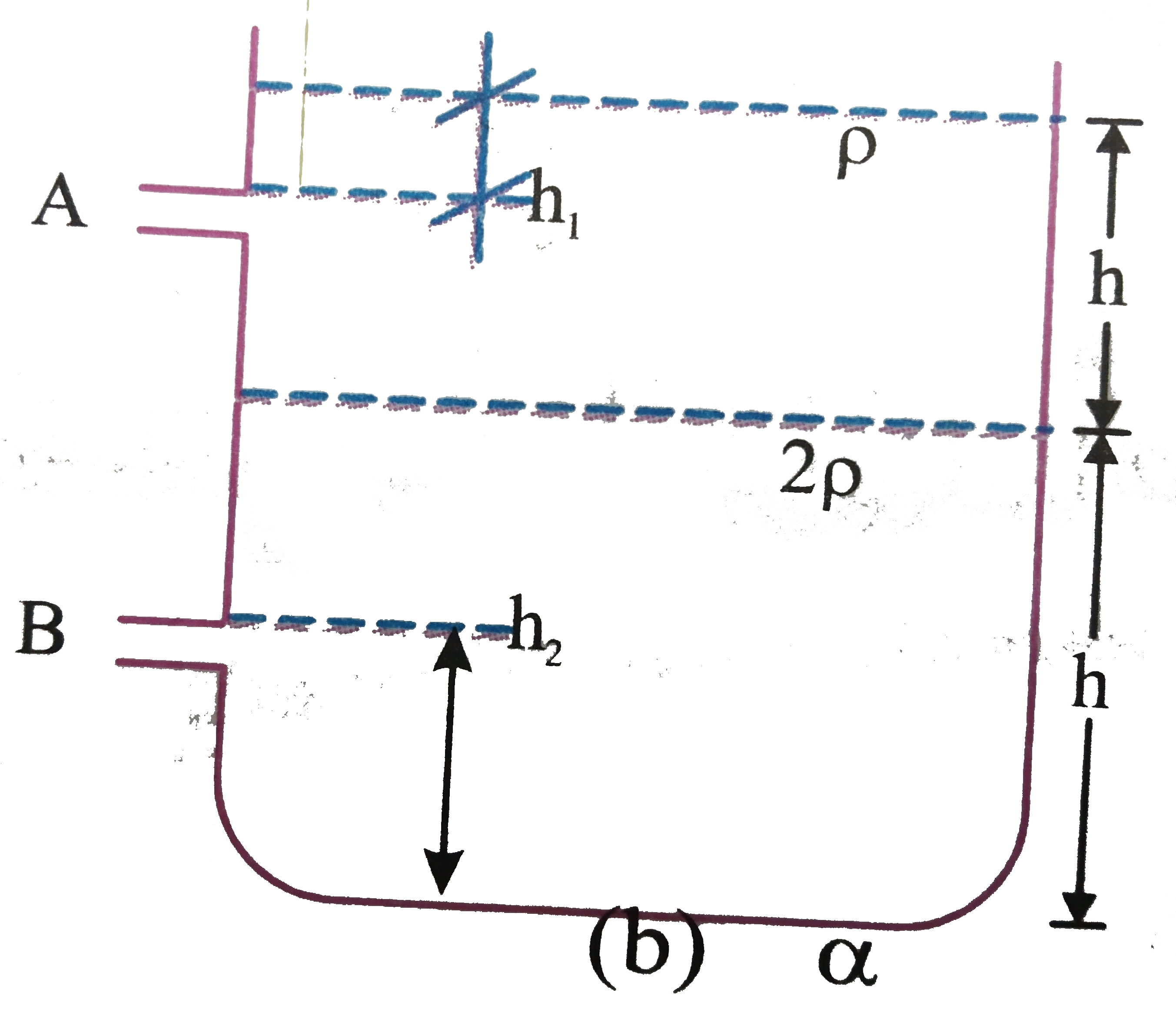
In the arrangement shown two liquids of density ρ and 2ρ are filled in a container the height of both liquids is h. there are two holes A and B at heights h1 and h2 from top liquid surface and bottom of the vessel. if V1 and V2 are the velocities of efflux at the two holes A and B respectively, find the correct graph.
Take =α(V2V1)2
View SolutionThe height to which a cylindrical vessel be filled with a homogenous liquid, to make the average force with which the liquid presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel, is equal to.
View SolutionA cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
View Solution
