The terminal velocity of a ball in air is v, where acceleration due to gravity is g. Now the same ball is taken in a gravity free space where all other conditions are same. The ball is now pushed at a speed v, then –
The terminal velocity of the ball will be v/2
The ball will move with a constant velocity
The initial acceleration of the ball is 2g in opposite direction of the ball's velocity
The ball will fanilly stop (Given that density of the ball ρ=2 times the density of are σ)
The correct Answer is:C
Step by step video, text & image solution for The terminal velocity of a ball in air is v, where acceleration due to gravity is g. Now the same ball is taken in a gravity free space where all other conditions are same. The ball is now pushed at a speed v, then – by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE-2 (ASSERTION AND REASON)28videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE-3 SECTION-A (PREVIOUS YEAR PROBLEM)61videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - QUESTIONS FOR PRACTICE6videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
- BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-4 (LEVEL-II)30videos
HEAT-2
- BOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 2)6videos
KINEMATICS
Similar Questions
A solid sphere moves at a terminal velocity of 20ms−1 in air at a place where g=9.8ms−2. The sphere is taken in a gravity free hall having air at the same pressure and pushed down at a speed of 20ms−1
View SolutionIf density (D), acceleration due to gravity (g) and frequency (v) are taken as base quantities , find the dimensions of force.
View Solution
Knowledge Check
- Question 1 - Select One
Time period of simple pendulum of length l at a place, where acceleration due to gravity is g and period T. Then period of simple pendulum of the same length at a place where the acceleration due to gravity 1.02 g will be
ATB1.02 TC0.99 TD1.01 T - Question 2 - Select One
If g is acceleration due to gravity at the equator when earth were at rest and g1 is acceleration due to gravity at the same place when earth spins with angular velocity ω, the relation between them is
Ag1=g(1−Rω2g)Bg1=g(1−Rω2)Cg1=g−R2ωDg=g1−R2ω - Question 3 - Select One
The terminal velocity v of a small steel ball ofradius r fal ling under gravity through a column ofa viscous liquid of coefficient of viscosity η depends on mass of the ball m, acceleration due to gravity g, coefficient of viscosity η and radius r. Which of the following relations is dimensionally correct?
Avr∝ηmgrBvr∝mgrηCvr∝mgrηDvr∝mg ηr
If rocket engine ejects fuel at the rate μ kg/s with relative velocity vr. At time t = 0, speed of rocket is u. Consider the value of acceleration due to gravity is constant and equal to g.
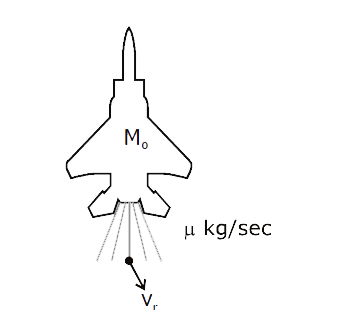
If rocket is in gravity free space then find velocity of rocket as function of time.View SolutionA rubber ball is dropped from a height of 5m on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to 1.8m. The ball loses its velocity on bouncing by a factor of
View SolutionFind the value of a and b in the following cases :
(a) The velocity v of the ball falling freely under gravity is proportional to gahb, where g is the acceleration due to gravity, h is the height from which the ball is dropped.
(b) The kinetic energy K of a rotating body is proportional to Iaωb where I is the moment if inertia and ω is the angular speed.
(c ) The time-period T of spring pendulum is proportiona to makb, where m is the mass of block attached to the spring and k is the spring constant.
The speed of sound v in a gaseous medium is proportional to Paρb, where P is the pressure and ρ is the density of medium.View SolutionTwo identical balls are interconnected with a massless and inextensible thread. The system is in gravity free space with the thread just taut. Each ball is imparted a velocity v, one towards the other ball and the other perpendicular to the first, at t=0. Then,
View SolutionA steel ball of mass m falls in a viscous liquid with terminal velocity v, then the steel ball of mass 8m will fall in the same liquid with terminal velocity
View Solution

