The maximum value of the block m2 for which the system will remain in equilibruim (coefficient of friction between block m1 and plane surface is μ, Pulley are mass less ) is :
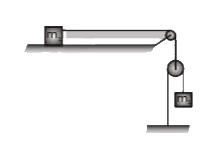
μm12
m12
μm1
2μm1
The correct Answer is:A
Step by step video & image solution for The maximum value of the block m_(2) for which the system will remain in equilibruim (coefficient of friction between block m_(1) and plane surface is mu, Pulley are mass less ) is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-266videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2(Level-II)25videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - SOLVED EXAMPLE16videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B12videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN12videos
ONE DIMENSION MOTION
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View Solution
Two blocks of mass M and 3M (in kg) are connected by an inextensible light thread which passes over a light frictionless pulley. The whole system is placed over a fixed horizontal table as shown.The coefficient of friction between the blocks and table surface is μ. The pulley is pulled by a string sttached to its centre and accelerated to left with acceleration a(ms2). Assume that gravity acts with constant acceleration g(ms2) downwards through the plane of table. Then:
(a) Find the forizontal accelration of both the blocks (Assume that both the blocks are moving.)
(b) What is the maximum acceleration a, for which the block of mass 3 M will remain stationary?View Solution
Knowledge Check
- Question 1 - Select One
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ - Question 2 - Select One or More
In the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.
 AThe maximum possible speed of the blocks is g(m2−μm1)√k(m1+m2)BThe maximum possible speed of the blocks is g(μm1)√k(m1+m2)CThe maximum possible speed of the blocks if friction is absent is gm2√k(m1+m2)DThe maximum possible speed of the blocks if friction is absent is gm1√k(m1+m2)
AThe maximum possible speed of the blocks is g(m2−μm1)√k(m1+m2)BThe maximum possible speed of the blocks is g(μm1)√k(m1+m2)CThe maximum possible speed of the blocks if friction is absent is gm2√k(m1+m2)DThe maximum possible speed of the blocks if friction is absent is gm1√k(m1+m2) - Question 3 - Select One
A spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
Aμ2m2g22kB2μm2g2kCμ2m2g2kD3μ2mg2k
Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?
 View Solution
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionIn the arrangement shown in the figure mass of the block B and A are 2m , 8m respectively. Surface between B floor is smooth. The block B is connected to block C by means of a pulley. If the whole system is released then the minimum value of mass of the block C so that the block A remains stationary with respect to B is: (Coefficient of friction between A and B is μ and pulley is ideal).
 View Solution
View SolutionFind the maximum value of (m//m) in the situation shown in figure so that the system remains at rest. Friction coefficient of both the contacts is μ , string is massless an pulley is friction less.
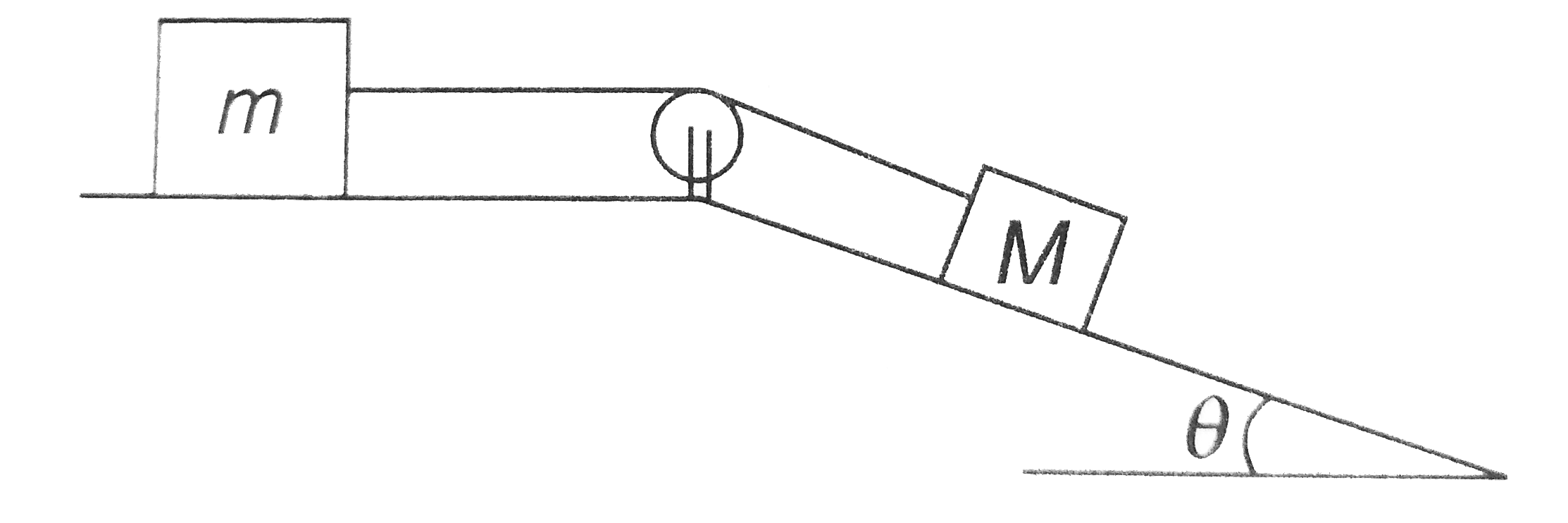 View Solution
View Solution

