A body is placed on a rough inclined plane of inclination θ. As the angle θ is increased from 0∘ to 90∘ the contact force between the block and the plane
remains constant
first remains constant then decreases
first decreases then increases
first increases then decreases
The correct Answer is:B
To analyze the contact force between a block and a rough inclined plane as the angle of inclination θ increases from 0∘ to 90∘, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
When the block is placed on the inclined plane, the forces acting on it are:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting perpendicular to the surface of the incline.
- The frictional force (f) acting parallel to the surface of the incline.
Step 2: Resolve the Gravitational Force
The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
Step 3: Analyze the Normal Force
The normal force N is equal to the component of the gravitational force acting perpendicular to the incline:
N=mgcosθ
Step 4: Analyze the Frictional Force
The frictional force f can be expressed as:
f=μN=μ(mgcosθ)
where μ is the coefficient of friction between the block and the inclined plane.
Step 5: Consider the Motion of the Block
As θ increases:
- At θ=0∘: The block does not experience any inclination, and the contact force is simply the normal force N=mg.
- As θ increases, the normal force decreases because N=mgcosθ.
- At θ=90∘: The incline becomes vertical, and the normal force approaches zero, meaning the block would no longer be in contact with the incline.
Step 6: Conclusion on Contact Force
As θ increases from 0∘ to 90∘:
- The normal force N decreases from mg to 0.
- The contact force between the block and the inclined plane also decreases from mg to 0.
Summary
The contact force between the block and the inclined plane decreases as the angle of inclination θ increases from 0∘ to 90∘.
When the block is placed on the inclined plane, the forces acting on it are:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting perpendicular to the surface of the incline.
- The frictional force (f) acting parallel to the surface of the incline.
The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
The normal force N is equal to the component of the gravitational force acting perpendicular to the incline:
N=mgcosθ
The frictional force f can be expressed as:
f=μN=μ(mgcosθ)
where μ is the coefficient of friction between the block and the inclined plane.
As θ increases:
- At θ=0∘: The block does not experience any inclination, and the contact force is simply the normal force N=mg.
- As θ increases, the normal force decreases because N=mgcosθ.
- At θ=90∘: The incline becomes vertical, and the normal force approaches zero, meaning the block would no longer be in contact with the incline.
As θ increases from 0∘ to 90∘:
- The normal force N decreases from mg to 0.
- The contact force between the block and the inclined plane also decreases from mg to 0.
The contact force between the block and the inclined plane decreases as the angle of inclination θ increases from 0∘ to 90∘.
Topper's Solved these Questions
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2
66 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2(Level-II)
25 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - SOLVED EXAMPLE
16 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN
12 Videos
Similar Questions
A block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View SolutionA block of mass m slides down a rough inclined plane of inclination θ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is μ with θ>tan−1(μ). Rate of work done by the force of friction at time t is
View Solution
Knowledge Check
A body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the contact force between the block and the plane
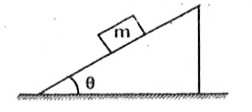 Aremains constantBdecreases.Cfirst decreases then increasesDfirst increases then decrease.
Aremains constantBdecreases.Cfirst decreases then increasesDfirst increases then decrease.A body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the normal force between the block and the plane is,
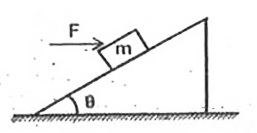 AF+mgtanθBFcosθ−mgsinθCFsinθ−mgcosθDFsinθ+mgcosθ
AF+mgtanθBFcosθ−mgsinθCFsinθ−mgcosθDFsinθ+mgcosθA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced if θ is reduced
A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View SolutionWhen a body is placed on a rough plane inclined at an angle θ to the horizontal, its acceleration is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block rests on a rough plane whose inclination θ to the horizontal can be varied. Which of the following graphs indicates how the friction force F between the block and the plane varies as θ is increased?
View SolutionA block of mass 0.1 kg is kept on an inclined plane whose angle of inclination can be varied from θ=30∘ to θ=90∘. The coefficient of friction between the block & the inclined plane is μ=1. A force of constant magnitude 12mg newton always acts on the block directed up the inclined plane and parallel to it. Then :
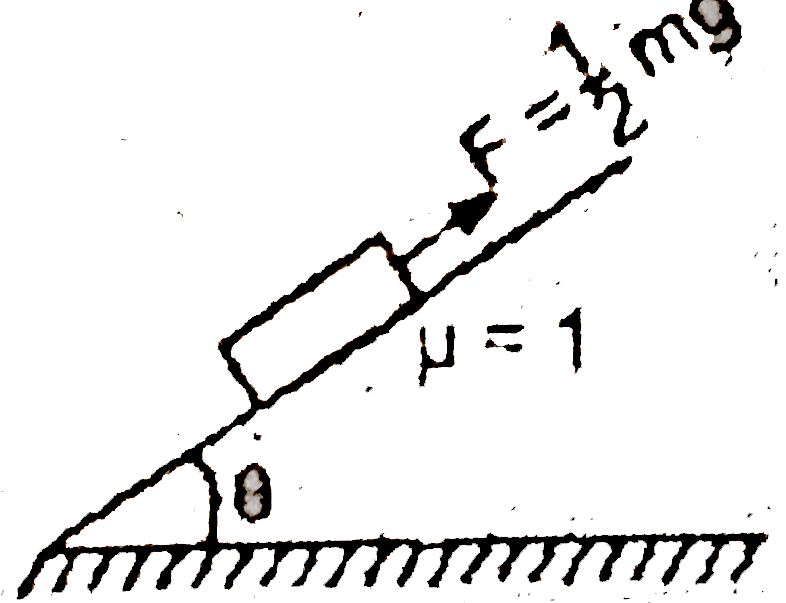
View Solution
