A block rests on a rough plane whose inclination $θ$ to the horizontal can be varied. Which of the following graphs indicates how the friction force $F$ between the block and the plane varies as $θ$ is increased?

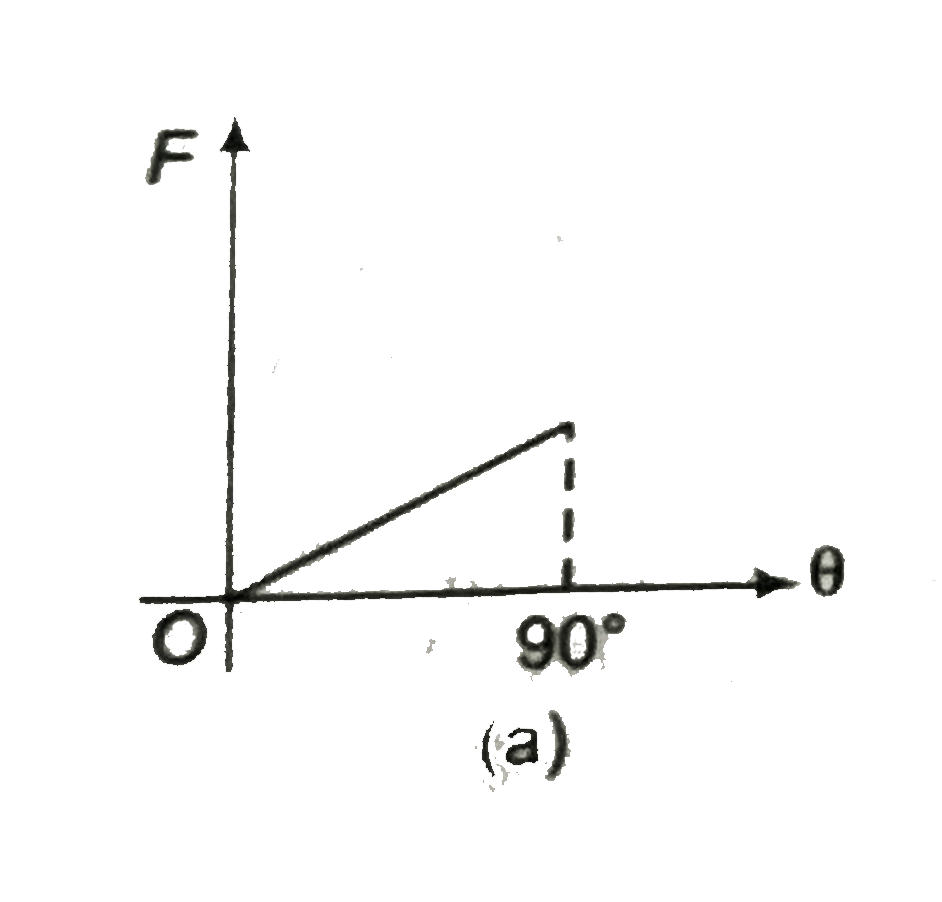
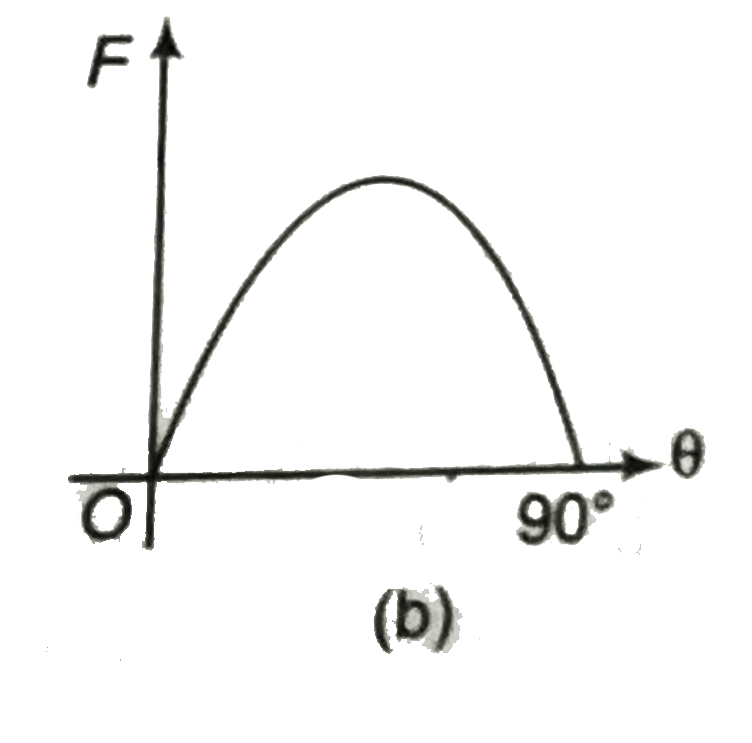
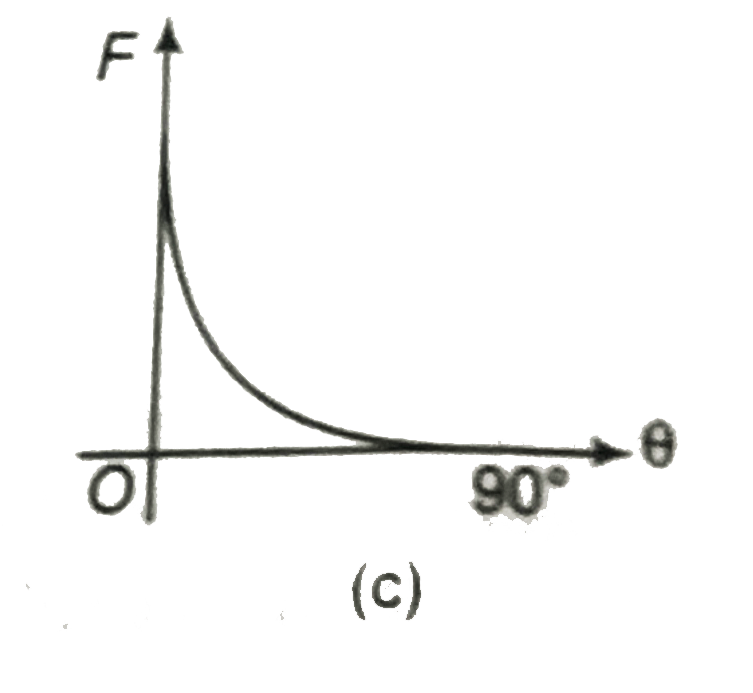
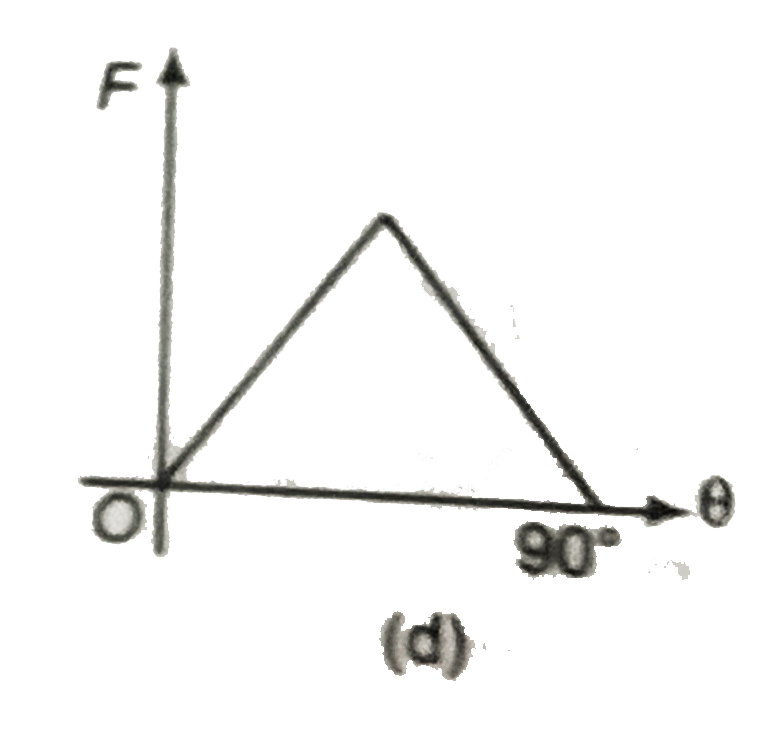
ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

A body is placed on a rough inclined plane of inclination $θ$ . As the angle $θ$ is the increased from $0^{\circ}$ to $90^{\circ}$ , the contact force between the block and the plane

Aremains constant
Bdecreases.
Cfirst decreases then increases
Dfirst increases then decrease.
A block of mass m slides down a rough inclined plane of inclination $θ$ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is $μ$ with $θ > {tan}^{- 1} (μ)$ . Rate of work done by the force of friction at time t is
A $μ m g^{2} t sin θ$
B $m g^{2} t (sin θ - μ cos θ)$
C $μ m g^{2} t cos θ (sin θ - μ cos θ)$
D $μ m g^{2} t cos θ$
A body is placed on a rough inclined plane of inclination $θ$ . As the angle $θ$ is the increased from $0^{\circ}$ to $90^{\circ}$ , the normal force between the block and the plane is,

A $F + m g tan θ$
B $F cos θ - m g sin θ$
C $F sin θ - m g cos θ$
D $F sin θ + m g cos θ$