A carpet of mass M made of inextensible material is rolled along its length in the form of a cylinder of radius R and is kept on a graph floor. The carpet. Starts unrolling without sliding on the floor when a negligible small push is given to it. Calculate the horizontal velcoity of the axis of the cylindrical part of the carpet when its radius reduces to R/2.
The correct Answer is:v=√14gR3
Step by step video & image solution for A carpet of mass M made of inextensible material is rolled along its length in the form of a cylinder of radius R and is kept on a graph floor. The carpet. Starts unrolling without sliding on the floor when a negligible small push is given to it. Calculate the horizontal velcoity of the axis of the cylindrical part of the carpet when its radius reduces to R//2. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - I)
24 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - II)
49 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 3 (Level - I)
27 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 4 (LEVEL - II)
14 Videos
Similar Questions
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View Solution
A rod of mass m and length 2 R is fixed along te diameter of a ring of same mass m and radius R as shown in figure. The combined body is rolling without slipping along x-axis find the angular momentum about z-axis.
View Solution
Knowledge Check
A floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
A25MgRB57MgRC78MgRDMgRA uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
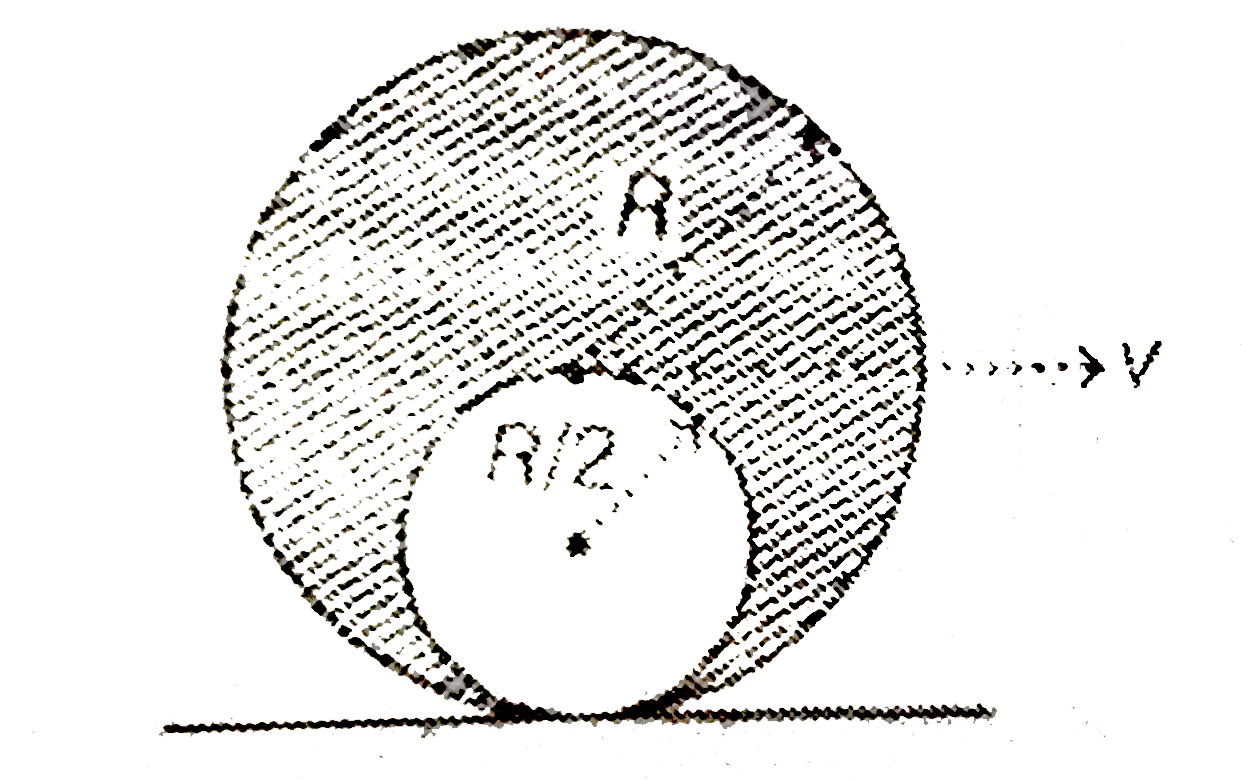 ATotal kinetic energy at this moment is 1516Mv2BTotal kinetic energy at this moment is 159Mv2CVelocity of centre of mass of the cylinder at this moment is 43vDVelocity of centre of mass of the cylinder at this moment is 76v
ATotal kinetic energy at this moment is 1516Mv2BTotal kinetic energy at this moment is 159Mv2CVelocity of centre of mass of the cylinder at this moment is 43vDVelocity of centre of mass of the cylinder at this moment is 76vA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
A√34ghB√43ghC√4ghD√2gh
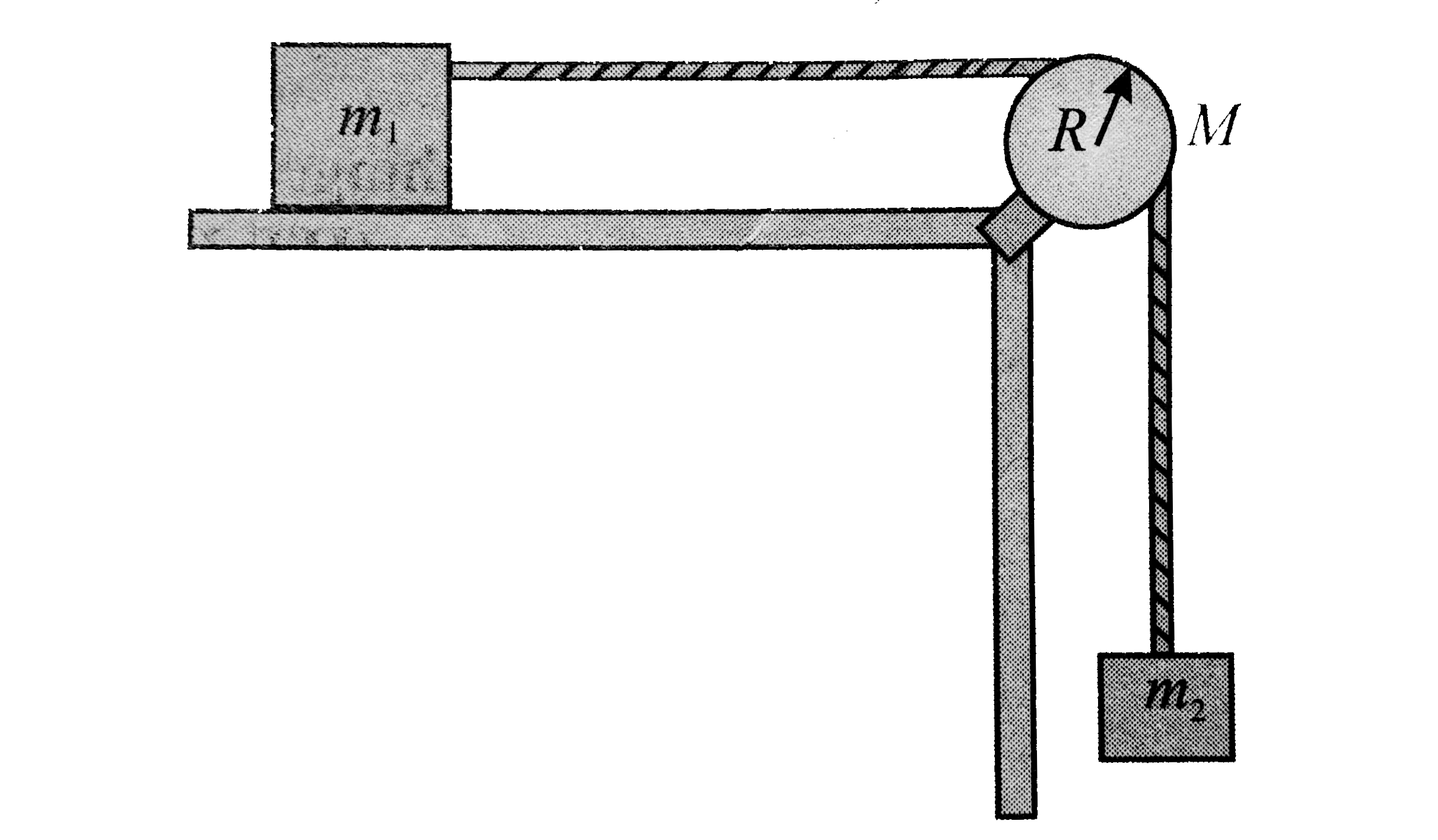
In figure mass m1 slides without friction on the horizontal surface, the frictionless pulley is in the form of a cylinder of mass M and radius R, and a string turns the pulley without slipping. Find the acceleration of each mass, and tension in each part of the string.
View SolutionA sphere of mass m and radius R is kept on a rough horizontal floor. Constant force Facts at the top point of sphere along tangent. If there is sufficient friction on the floor to support pure rolling then calculate acceleration of sphere.
View SolutionA sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
View SolutionA wheel of radius R is rolling without sliding uniformly on a horizontal surface. Find the radius of curvature of the path of a point on its circumference when it is at highest point in its path.
View SolutionFind the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View Solution
