A nonconducting disk of radius a and uniform positive surface charge density σ is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disk, from a height H with zero initial velocity. The particle has q/m=4ε0g/σ.
(i) Find the value of H if the particle just reaches the disk.
(ii) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
The correct Answer is:x=a/√3
Step by step video, text & image solution for A nonconducting disk of radius a and uniform positive surface charge density sigma is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disk, from a height H with zero initial velocity. The particle has q//m = 4 epsilon_(0) g// sigma. (i) Find the value of H if the particle just reaches the disk. (ii) Sketch the potential energy of the particle as a function of its height and find its equilibrium position. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 3 (Level -I) (Section F)
7 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 3 (Level -II) (Section A)
6 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 3 (Level -I) (Section D)
4 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)
30 Videos
Similar Questions
A dielectric disc of radius R and uniform positive surface charge density σ is placed on the grup with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc from a height H with dropped, along the axis of the disc from a height H with zero intial velocity. The charge -mass ratio of the particle is qm=4εon0gσ.
(i). Find the value of H if the particle just reaches the disc.
(ii). Sketch the potential energy of the particle as a function of its height and find its height in equilibrium position.
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View Solution
Knowledge Check
A uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
ADuring motion , NgtmgBDuring motion, normal reactions acts on the center of massCduring motion, the normal reaction shifts towards positive x-axis from the center of massDduring motion, normal reaction shifts in the direction of the force of friction.A long solenoid carrying a current I is placed with its axis vertical as shown in the figure. A particle of mass m and charge q is released from the top of the solenoid. Its acceleration is (g being acceleration due to gravity)
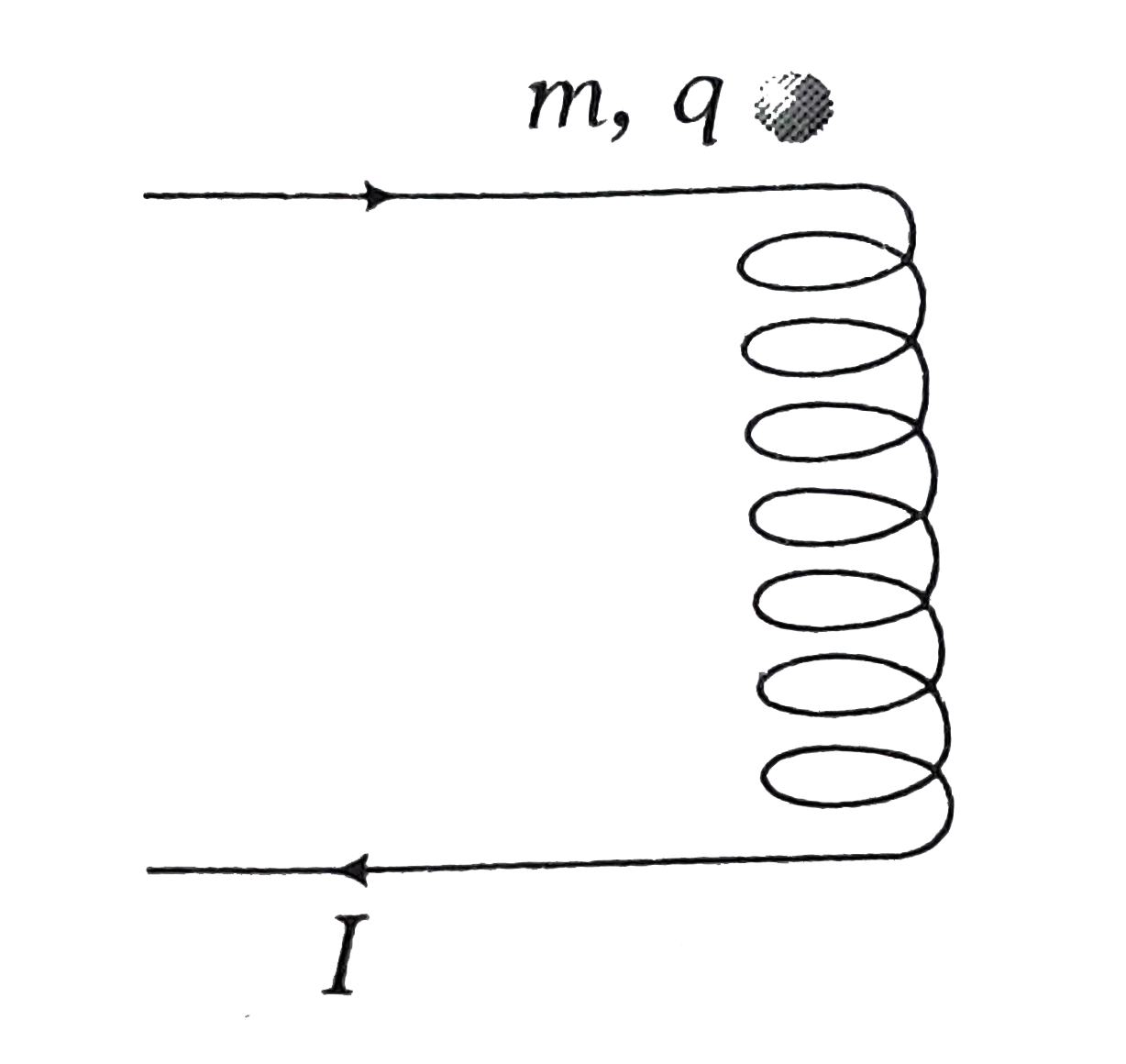 Agreater than gBless than gCequal to gDNone of these
Agreater than gBless than gCequal to gDNone of theseA thin circular disk of radius R is uniformly charged with density σ>0 per unit area.The disk rotates about its axis with a uniform angular speed ω.The magnetic moment of the disk is :
AπR4σωBπR42σωCπR44σωD2πR4σω
Charged Disk
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P (R√3,0,0) on the positive x-axis directly towards O, with an initial speed v. Find the smallest (non-zero) value of the speed v such that the particle does not return to P.
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
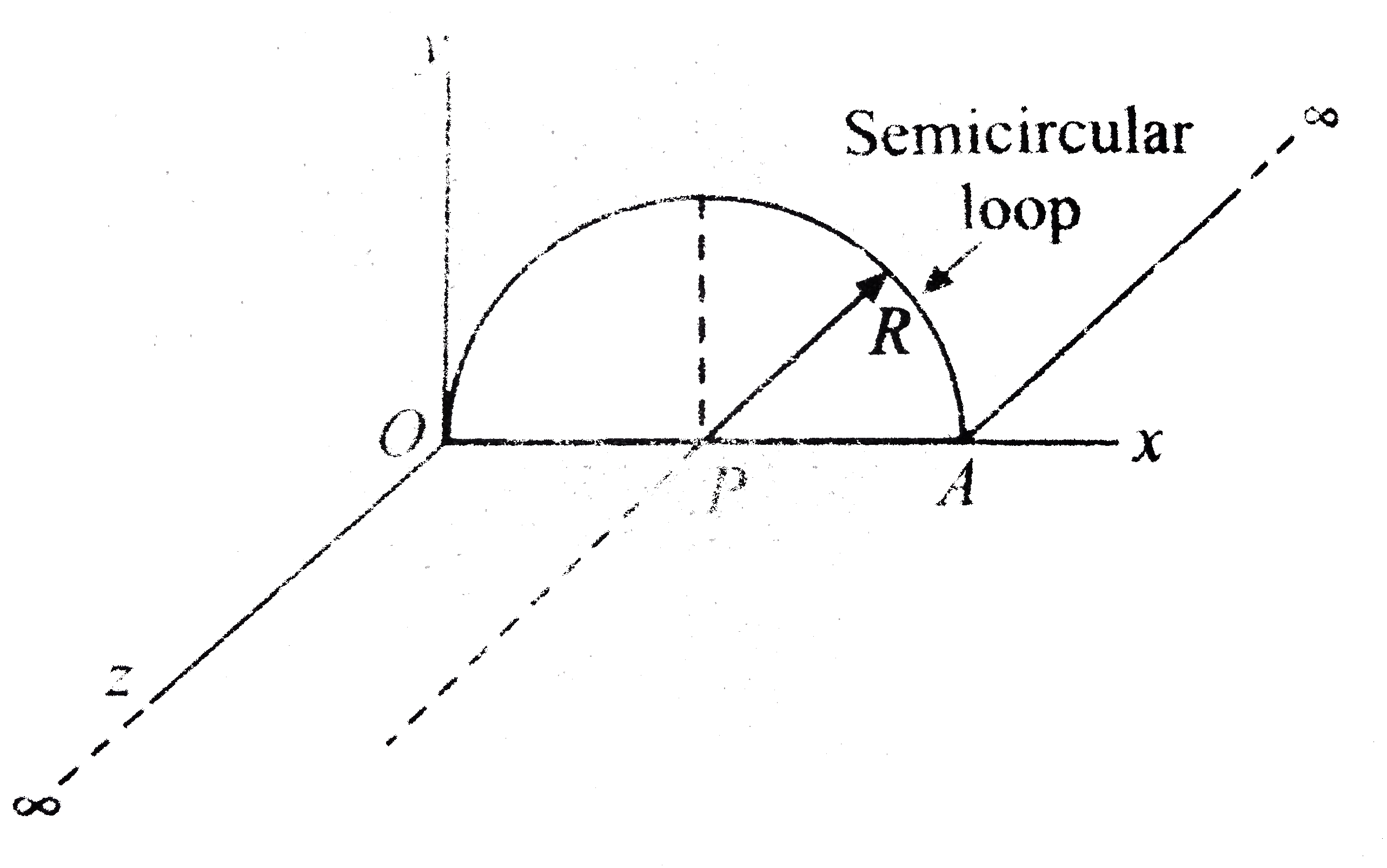
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View Solution
