A dielectric disc of radius R and uniform positive surface charge density σ is placed on the grup with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc from a height H with dropped, along the axis of the disc from a height H with zero intial velocity. The charge -mass ratio of the particle is qm=4εon0gσ.
(i). Find the value of H if the particle just reaches the disc.
(ii). Sketch the potential energy of the particle as a function of its height and find its height in equilibrium position.
The correct Answer is:(i) H=43R
(ii). H=R√3
Topper's Solved these Questions
Similar Questions
A nonconducting disk of radius a and uniform positive surface charge density σ is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disk, from a height H with zero initial velocity. The particle has q/m=4ε0g/σ.
(i) Find the value of H if the particle just reaches the disk.
(ii) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
View SolutionA nonconducting disk of radius a and uniform positive surface charge density σ is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disk, from a height H with zero initial velocity. The particle has q/m=4ε0g/σ.
(i) Find the value of H if the particle just reaches the disk.
(ii) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density σ. About its central axis of rotation it rotates at an angular speed ω. Find the magnetic moment of disc due to rotation of charges.
View SolutionA uniform disc of radius R is charged with a uniform surface charge density σ. Find the electric potential due to the charges on the disc at a point on its edge. [σRπ∈0]
View SolutionA point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then R=√3b.
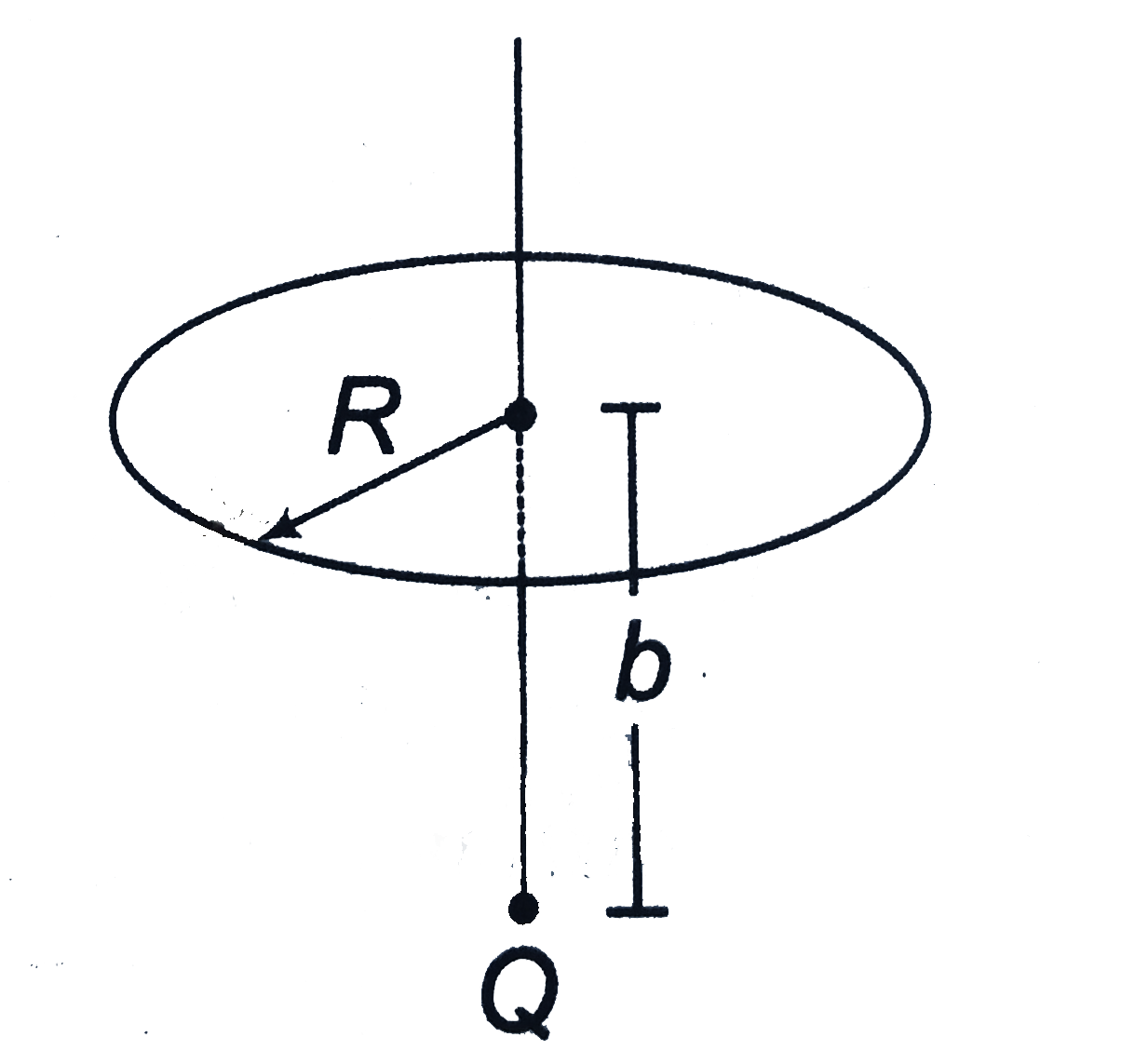
View SolutionA point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then R=√3b.

View SolutionA charged disc of radius 3 m has charge density σ. Electric field at a distance of 4 m from its centre on axis is _______
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View Solution
