Find how the voltage across the capacitor C varies with time t after closing of the switch Sw at the moment t=0.
.
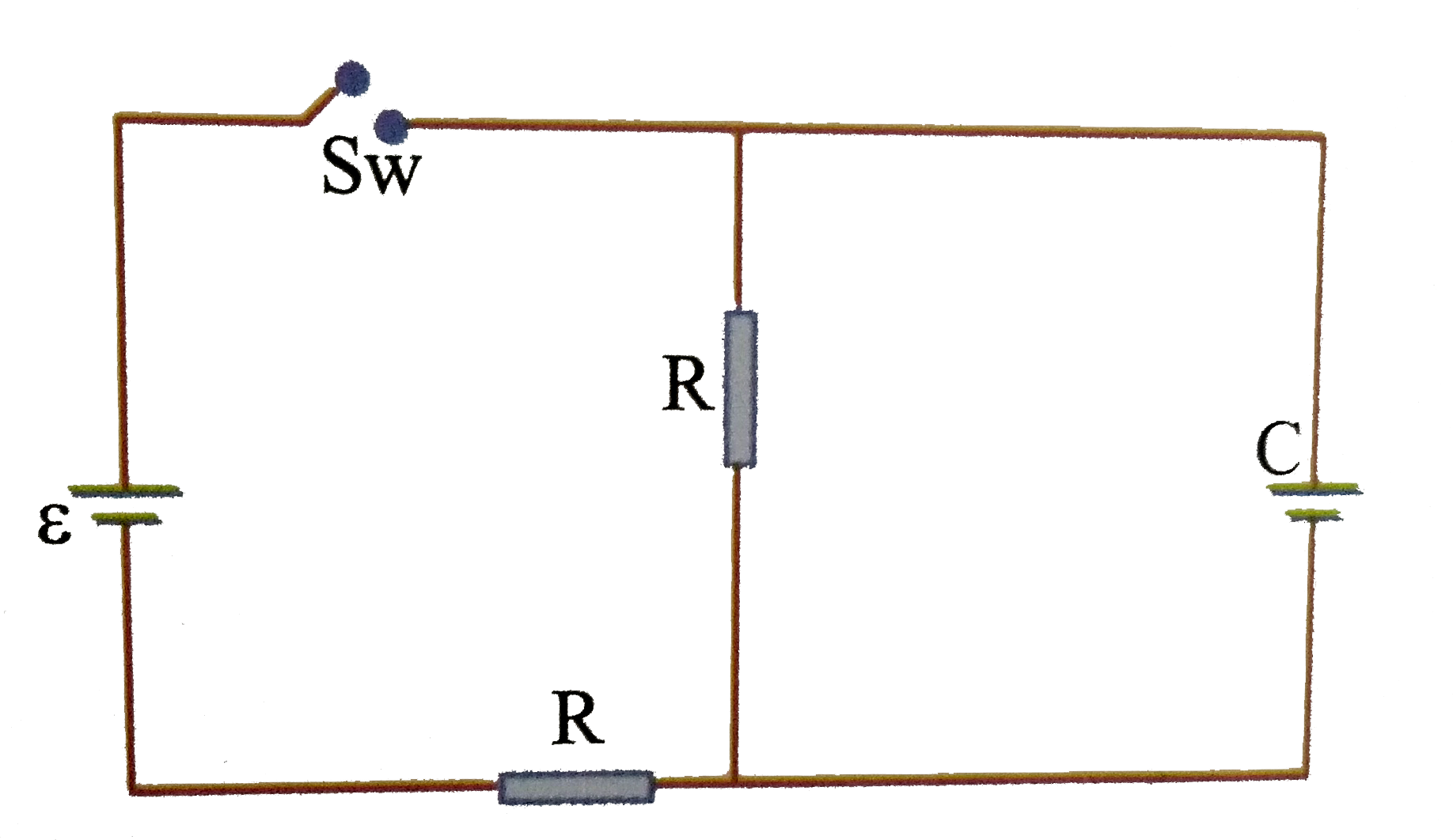The correct Answer is:V=∈2(1−e2t/RC)
Step by step video, text & image solution for Find how the voltage across the capacitor C varies with time t after closing of the switch S_(w) at the moment t=0. . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL 1
15 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -3 LEVEL 1
31 Videos
- CALORIMETRY BOOK - MOTIONCHAPTER - CALORIMETRY EXERCISE - EXERCISE - 3 Section - B
4 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
Similar Questions
A certain oscillating circuit consits of a capacitor with capacitance C, a coil with inductance L and active resistance R, and a switch . When the swith was disconnected, the capacitor was charged, then the switch was closed and oscillations set in. Find the ratio of the voltage across the capacitor to its peak value at the moment immediatel after closing the switch.
View SolutionA capacitor with an initial potential difference of 80.0 V is discharged through a resistor when a switch between them is closed at t=0. At t= 10.0s, the potential difference across the capacitor is 1.00V (a) What is time constant of the circuit? (b) What is the potential difference across the capacilor
View Solution
Knowledge Check
Find heat produced in the capacitors after long time on closing the switch S
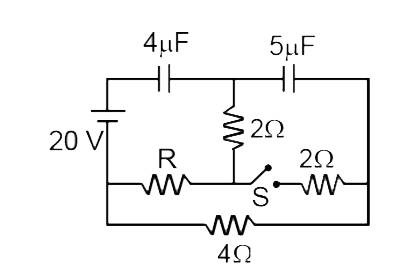A0.0002JB.0005JC0.00075JDzeroA capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by
AC0(V0−V)V0BC0(V−V0)V0CC0(V+V0)VDC0(V0−V)VIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is
A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μC
In the circuit shown in figure-3.244, the battery is an ideal one with emf V. The capacitor is initially uncharged. The switch S is closed at time t=0.
(a) Find the charge Q on the capacitor at time l
(b) Find the current in branch AB at time just after closing the switch.
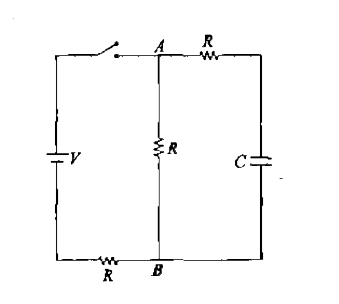View SolutionA 1−kΩ resistor is connected in series with a 10−mH inductor, a 30V battery and an open switch. At time t=0, the switch is suddenly closed.
a. What is the maximum current in this circuit and when does it occur?
b. What are the voltage drops across the inductor and across the resistor 20μs after the switch is closed?
c. On a single set of axes, sketch the voltage across the resistor and the voltage across the inductor as functions of time. Also, sketch a graph of the current in the circuit as s function of time.
View SolutionIn the circuit shown switches S1 and S2 have been closed for 1sec and S2 remained open.Just after 1 second is over switch S2 is closed and S1,S3 are opened.Find after that instant The charge on the upper plate of the capacitor as function of time taking the instant of switching on of S2 and switching off all time switches to be t=0 is q=x×10−2cos(t+π4).Findout value of x.
View SolutionIn the circuit shown in the figure, E=50.0V,R=250Ω and C=0.500μF. The switch S is closed for a long time, and no voltage is measured across the capacitor. After the switch is opened, the voltage across the capacitor reaches a maximum value of 150V. What is the inductance L?
View SolutionIn the circuit shown in fig. the switch is kept closed in position 1 for a long time. At time t=0 the switch is moved to position 2. Write the dependence of voltage (VC) across the capacitor as a function of time (t). Take VC to be positive when plate a is positive.
Given: R1=20Ω,R2=60Ω,R3=400kΩ,V1=40V,V2=90VandC=0.5μF.
View Solution