The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side.
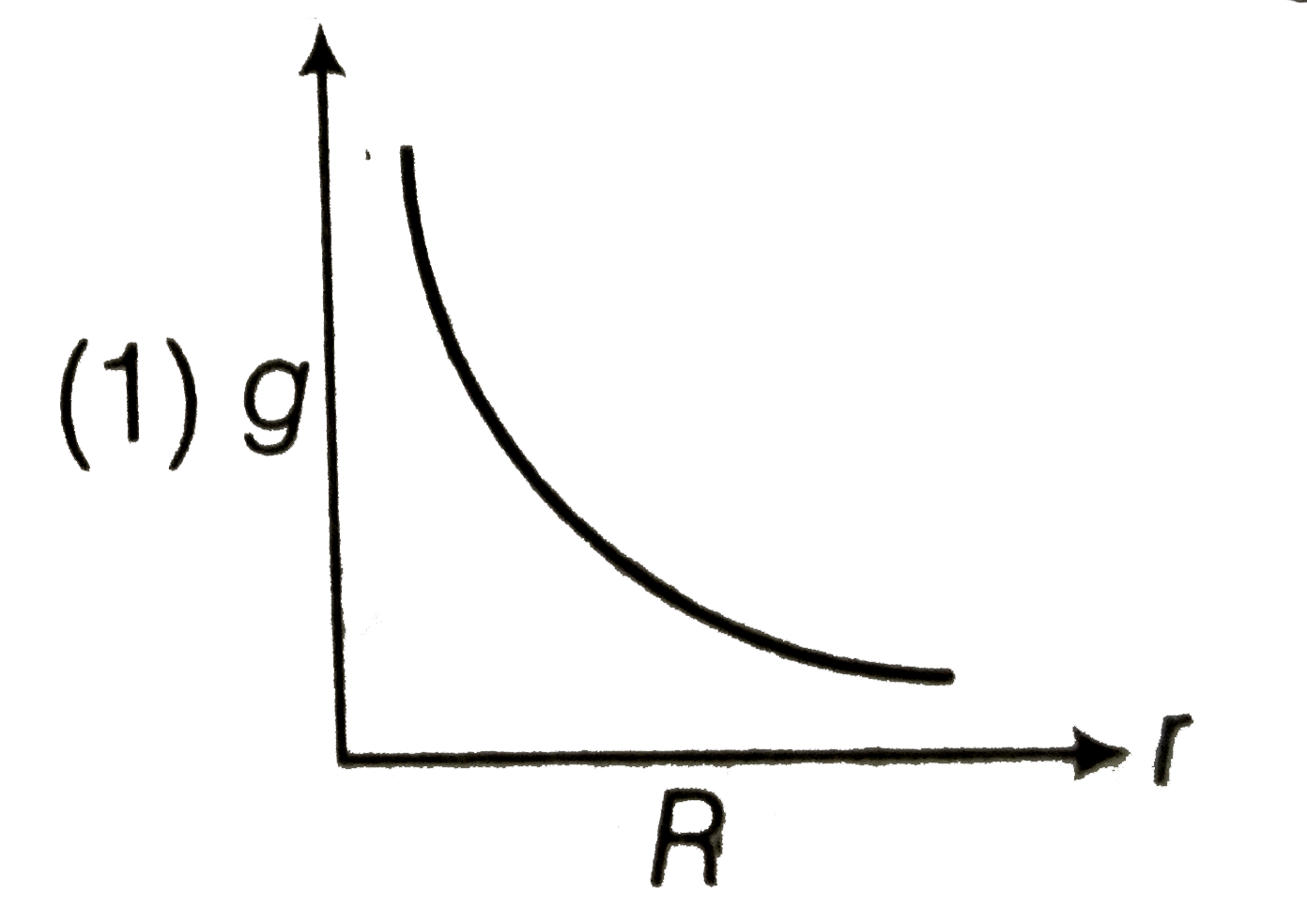
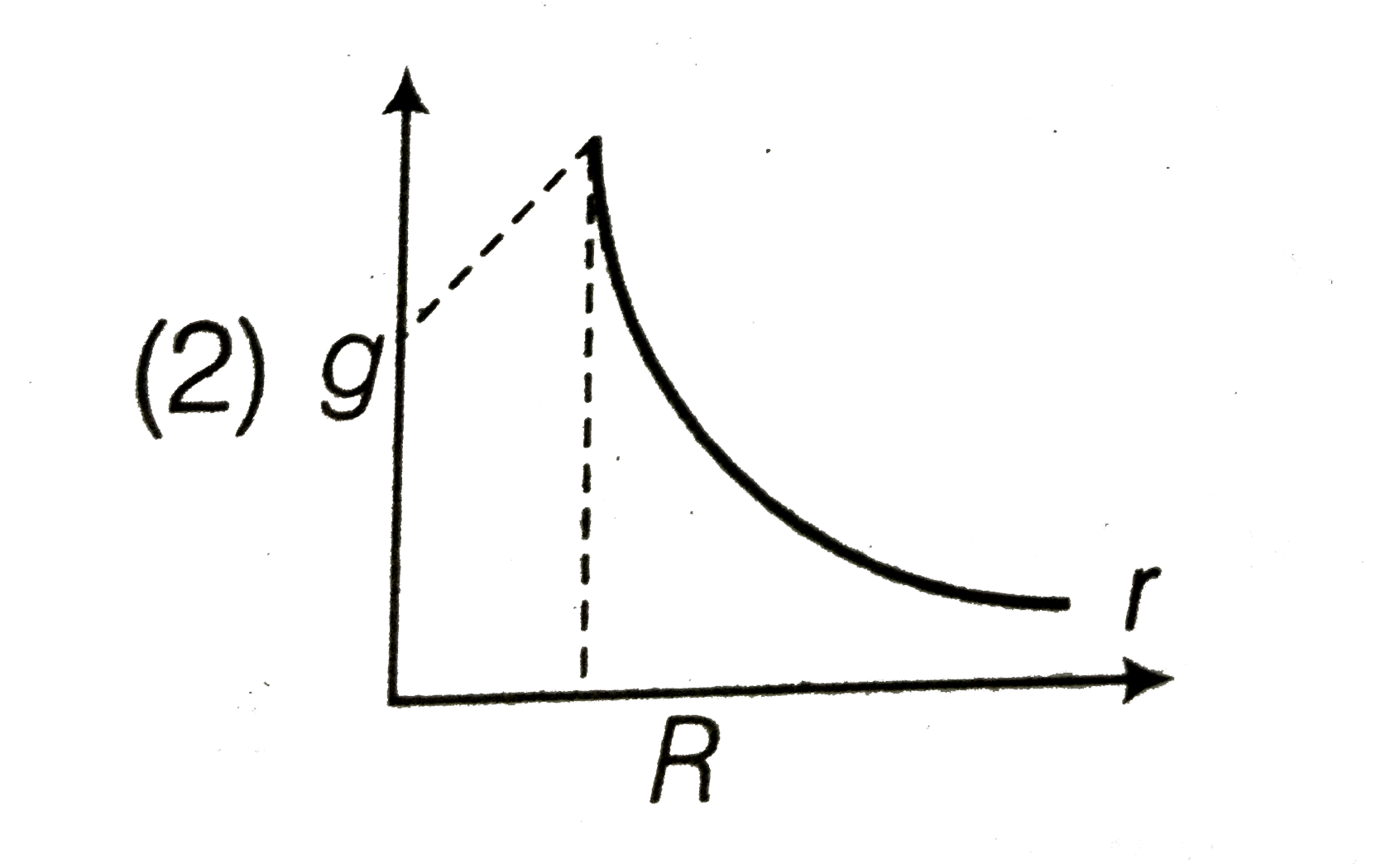
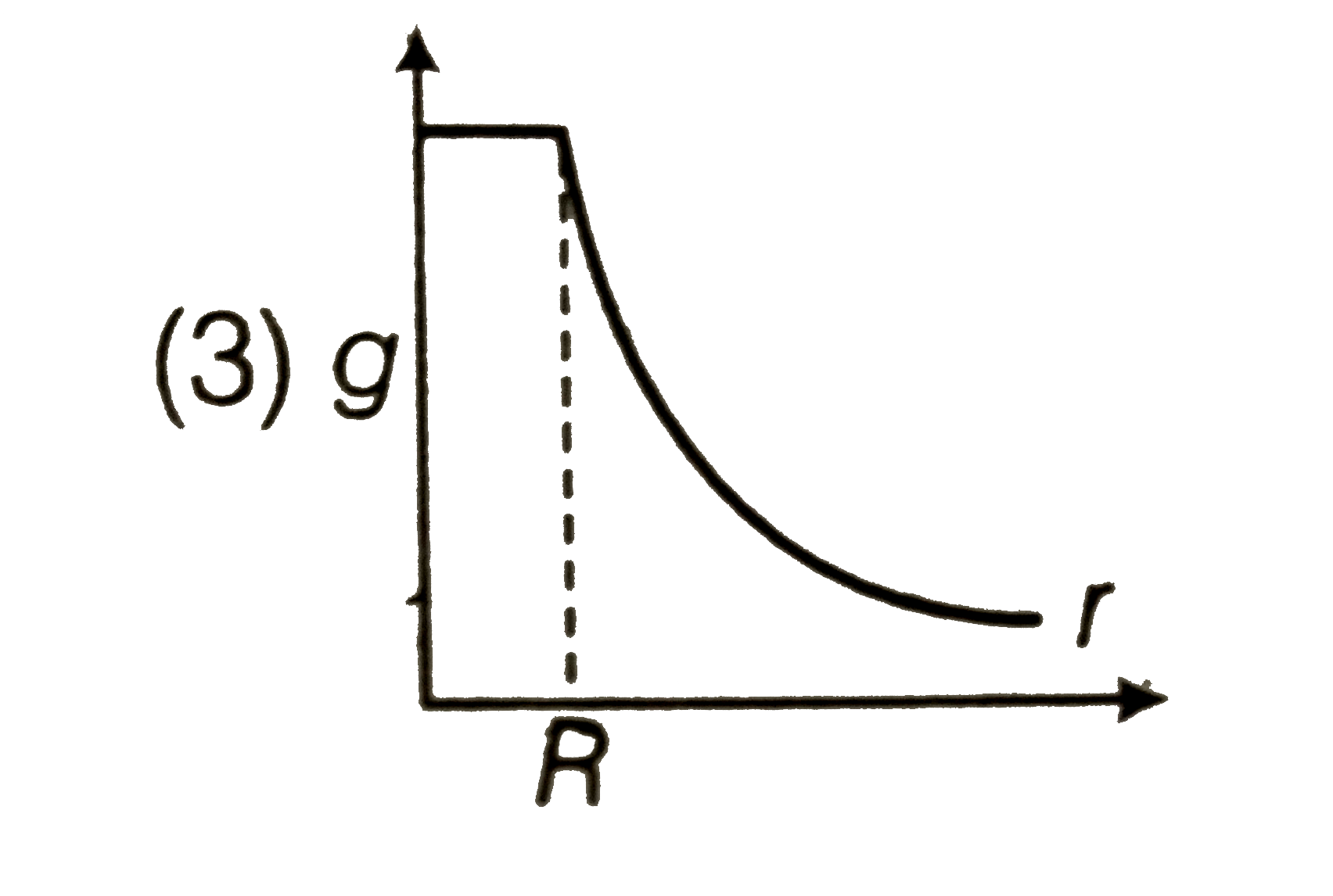
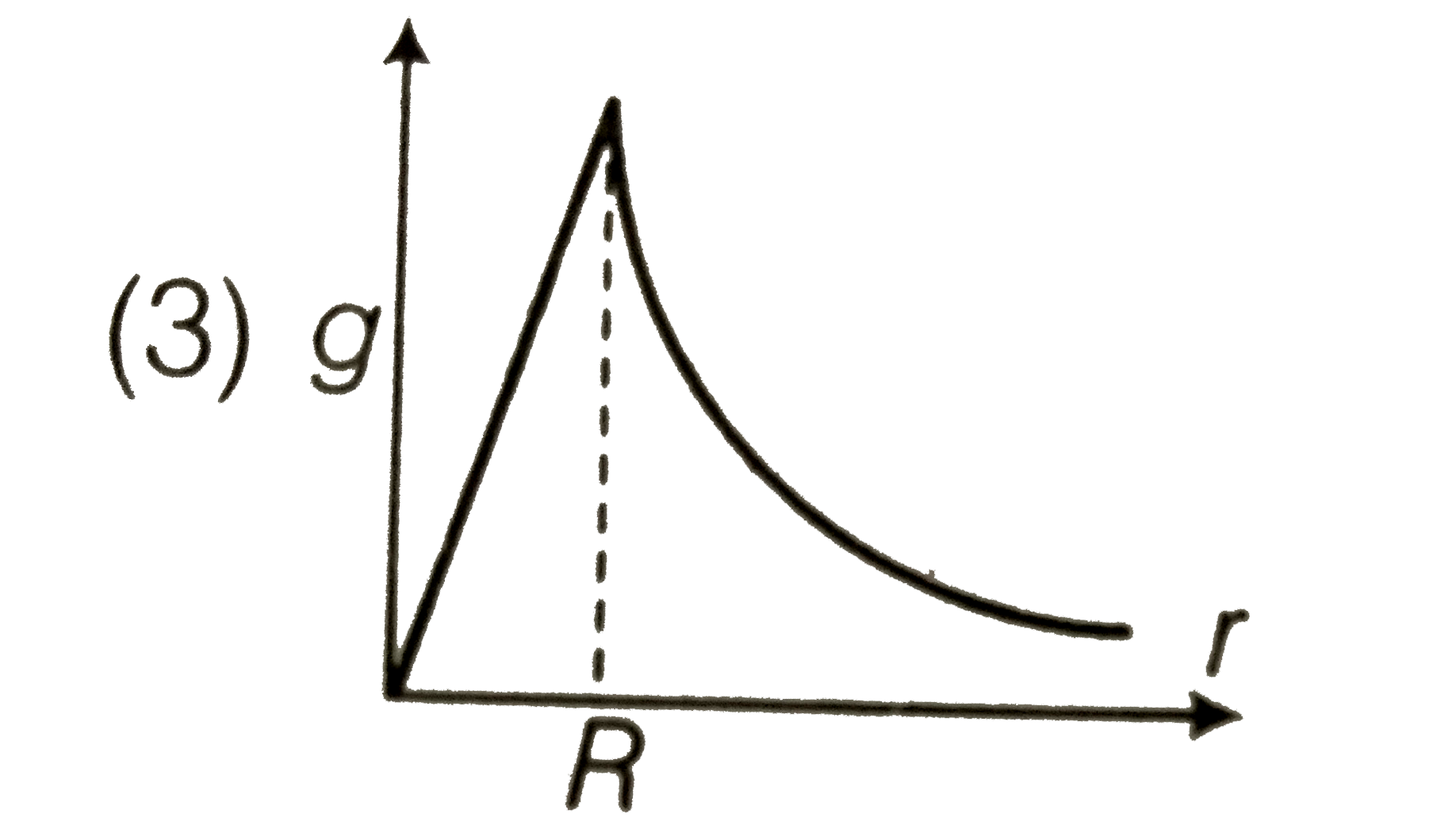
The correct figure is
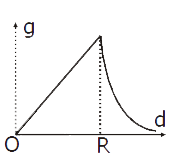
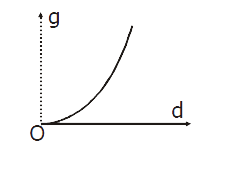
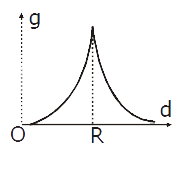
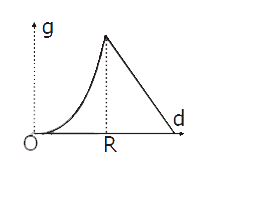
The correct Answer is:A
Step by step video, text & image solution for The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side. The correct figure is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 Section - A Previous Years Problems23videos
GRAVITATION
- BOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II55videos
GEOMETRICAL OPTICS
- BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced22videos
HEAT - 1
Similar Questions
Knowledge Check
- Question 1 - Select One
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to br a sphere of radius R of uniform density is as shoen in Fig. below:

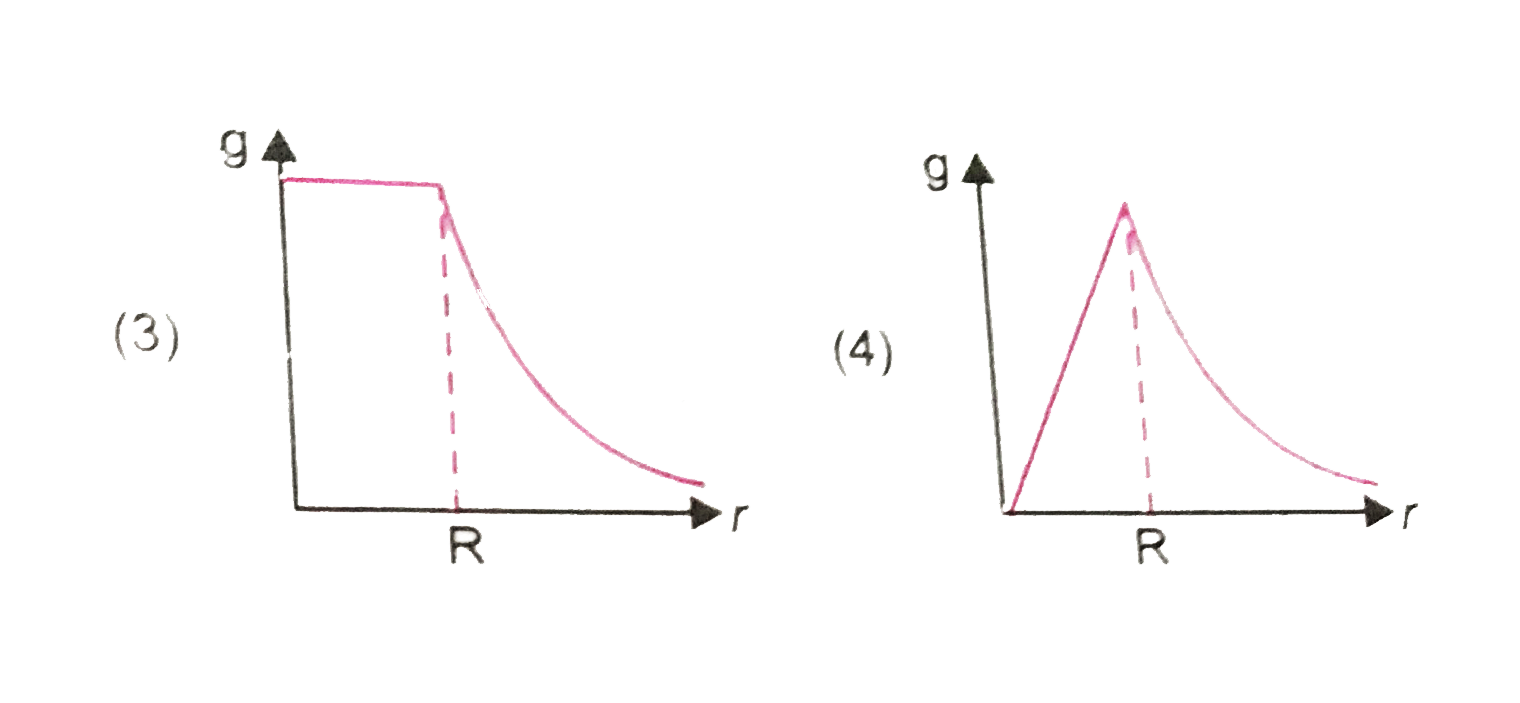
The correct figure isA(4)B(1)C(2)D(3) - Question 2 - Select One
Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
A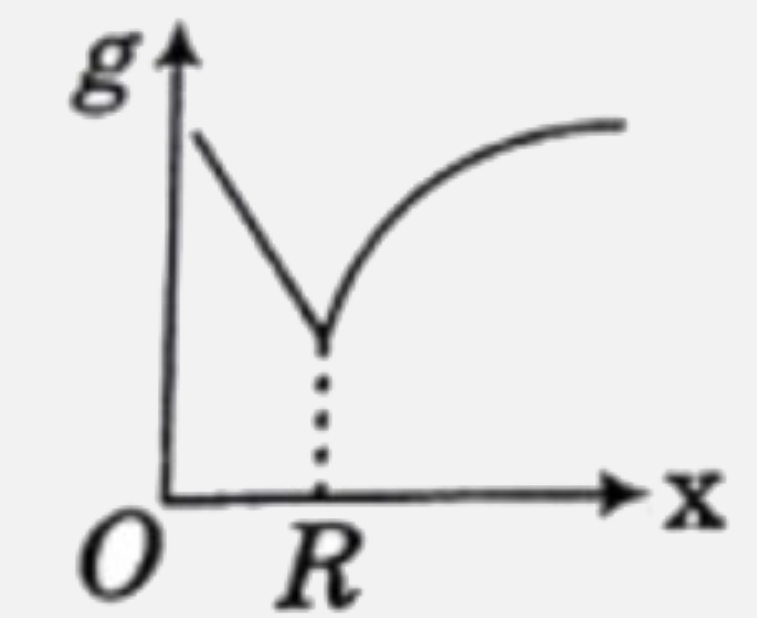 B
B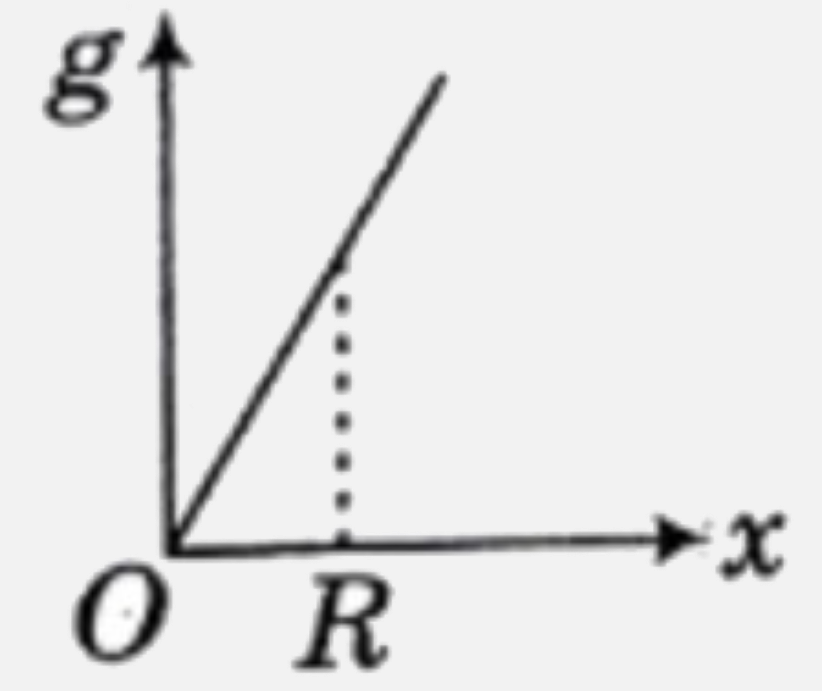 C
C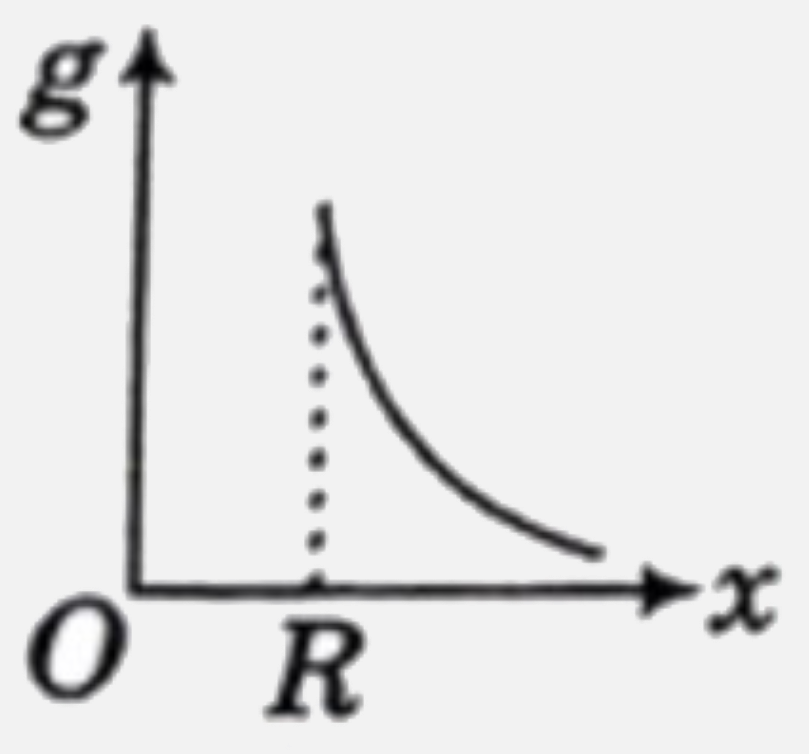 D
D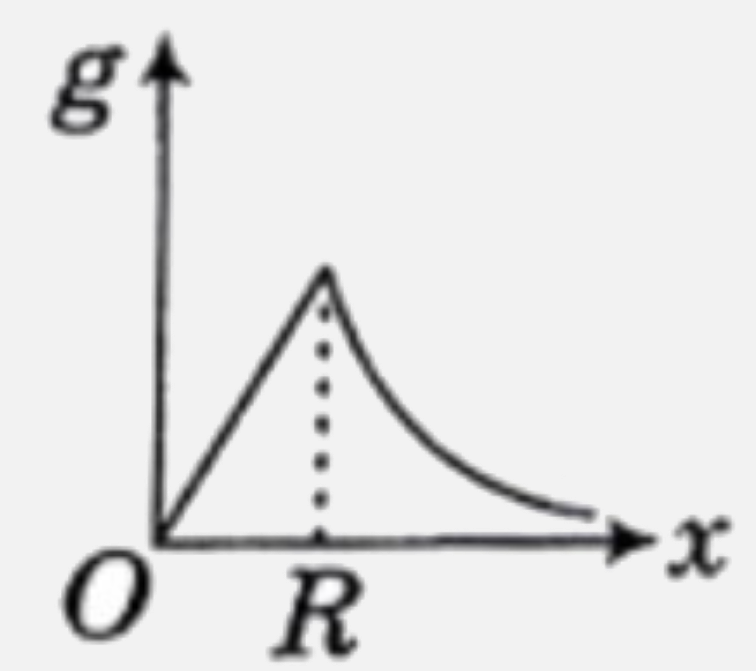
- Question 3 - Select One
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
Ag∝rBg∝r2Cg∝r−1Dg∝r−2
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
View SolutionIf g denotes the value of acceleration due to gravity at a point distance r from the centre of earth of radius R. If r<R, then
View SolutionThe value of g (acceleration due to gravity) at earth's surface is 10ms−2. Its value in ms−2 at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
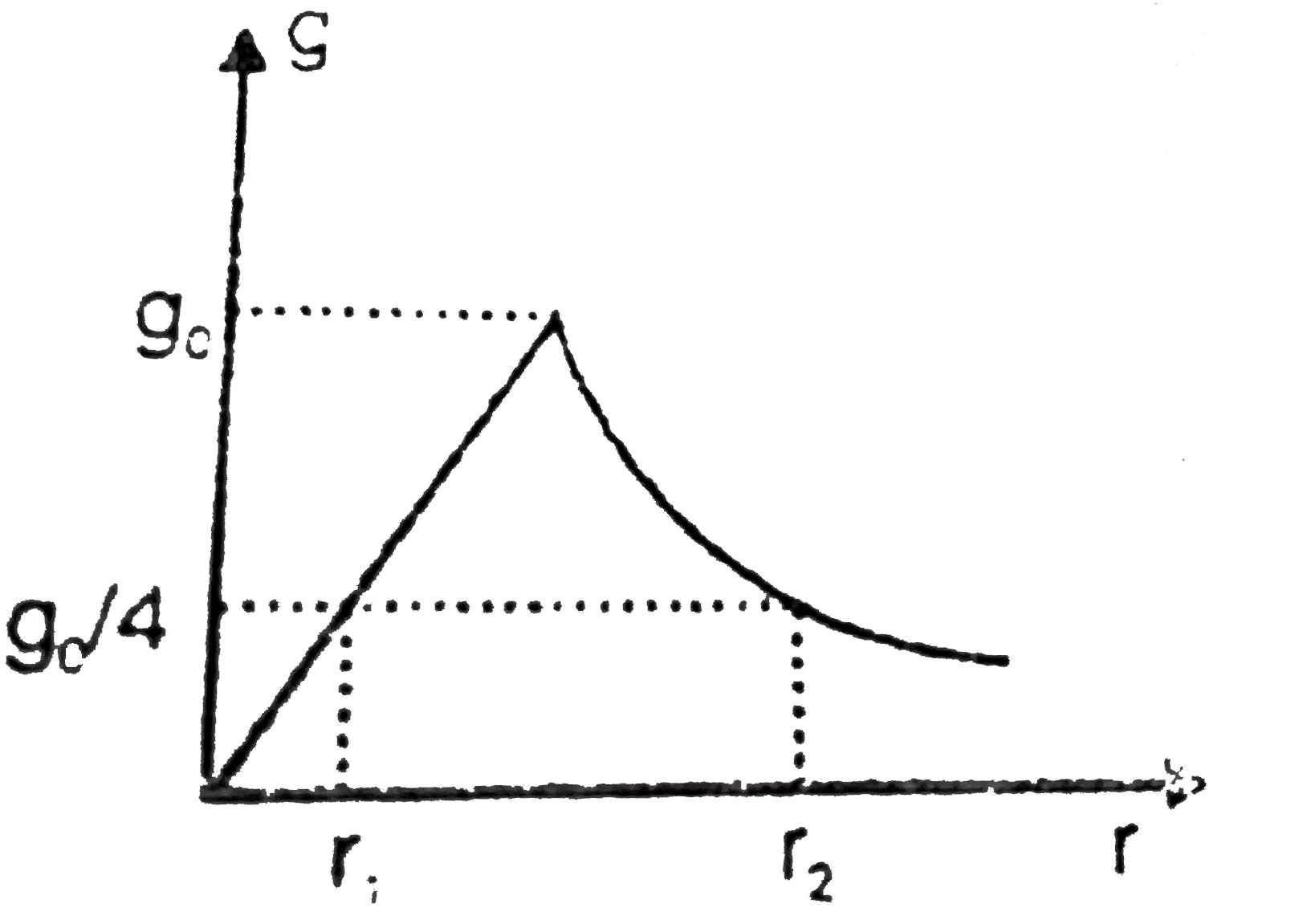 View Solution
View SolutionAssume the earth to be a sphere of uniform density the accleration due to gravity
View Solution

