Consider the graph of the function f(x)=x√|x| Statement-1: The graph of y=f(x) has only one critical point Statement-2: f'(x) vanishes only at one point
Step by step video & image solution for Consider the graph of the function f(x) = x sqrt|x| Statement-1: The graph of y=f(x) has only one critical point Statement-2: fprime (x) vanishes only at one point by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isA B
B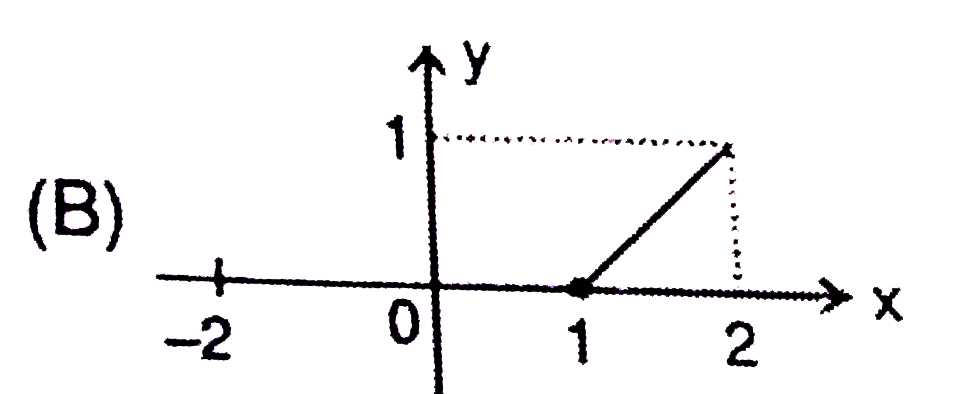 C
C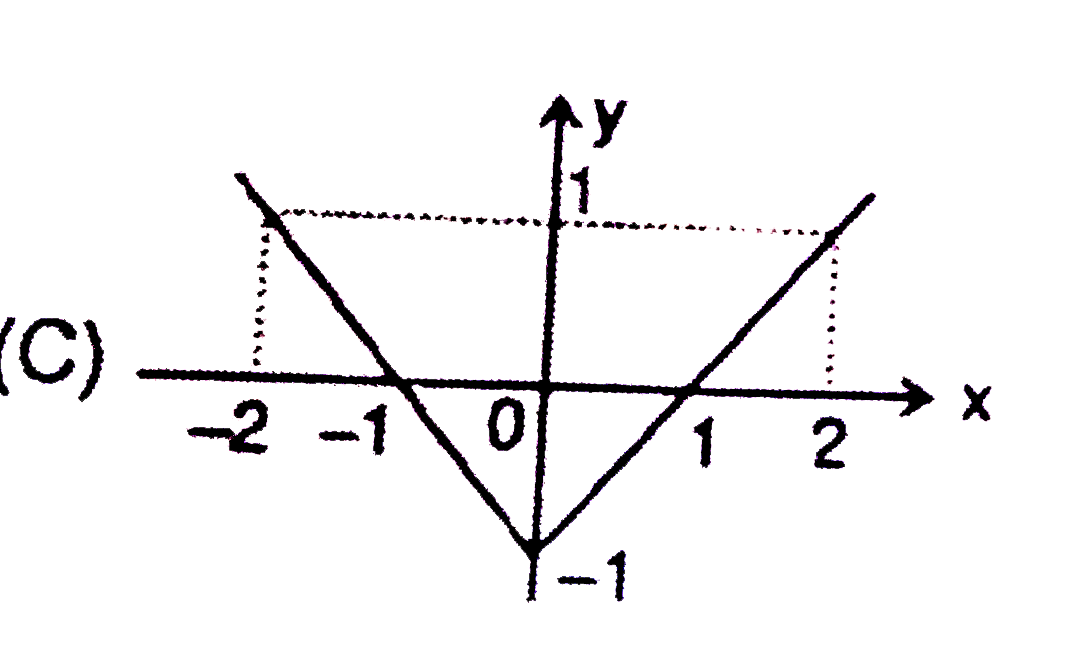 D
D
Consider f(x)=xx2−1
Statement I Graph of f(x) is concave up for x>1.
Statement II If f(x) is concave up then f''(x)>0ABoth statement I and Statement II are correct and Statement II is the correct explanation of Statement IBBoth Statement I and Statement II are correct but Statement II is not the correct explanation of Statement ICStatement I is correct but Statement II is incorrectDStatement II is correct but Statement I is incorrect.
If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) is
View SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) is
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionNumber of critical point of the function f(X) =x+√|x| is _______.
View SolutionNumber of critical point of the function f(X) =x+√|x| is _______.
View SolutionConsider f(x)=xx2−1
Statement I Graph of f(x) is concave up for x>1.
Statement II If f(x) is concave up then f''(x)>0
View Solution
