Bailey's Boutique Clothing is having a 20% off sale during which shirts cost $30.00 and pants cost $60.00. On the day of the sale, Bailey's sells a total of 60 shirts and pants and earned a total of $2,250. On a regular day, Bailey's sells 23 the number of shirts and pants sold during the sale and earns a total of $1,875. Solving which of the following system of equations yields the number of shirts,s, and the number of pants,p, sold during a regular day?
s+p=40
37.5s+75p=1,875
s+p=40
30s+60p=2,250
s+p=60
30s+60p=2,250
s+p=2,250
30s+60p=60
The correct Answer is:A
To solve the problem, we need to establish the equations based on the information provided about the sale and the regular day sales at Bailey's Boutique Clothing.
Step 1: Determine the equations for the sale day
1. Total items sold during the sale:
- Let s be the number of shirts sold and p be the number of pants sold.
- According to the problem, the total number of shirts and pants sold during the sale is 60.
- Therefore, we can write the first equation as:
s+p=60
2. Total revenue earned during the sale:
- Shirts are sold for $30 each and pants for $60 each.
- The total revenue from selling shirts and pants during the sale is $2,250.
- Thus, we can write the second equation as:
30s+60p=2250
Step 2: Determine the equations for a regular day
1. Total items sold on a regular day:
- It is given that on a regular day, Bailey's sells 23 of the total items sold during the sale.
- Therefore, the total number of shirts and pants sold on a regular day is:
s+p=23×60=40
2. Total revenue earned on a regular day:
- We need to find the regular prices of shirts and pants.
- Since shirts are sold at a 20% discount for $30, the original price X of a shirt can be calculated as follows:
X−0.2X=30⟹0.8X=30⟹X=300.8=37.5
- Similarly, for pants sold at a 20% discount for $60:
Y−0.2Y=60⟹0.8Y=60⟹Y=600.8=75
- Therefore, the revenue equation for a regular day, where s shirts and p pants are sold, is:
37.5s+75p=1875
Step 3: Formulate the system of equations
Now we have the following system of equations for a regular day:
1. s+p=40
2. 37.5s+75p=1875
Conclusion
The correct system of equations that yields the number of shirts s and the number of pants p sold during a regular day is:
1. s+p=40
2. 37.5s+75p=1875
1. Total items sold during the sale:
- Let s be the number of shirts sold and p be the number of pants sold.
- According to the problem, the total number of shirts and pants sold during the sale is 60.
- Therefore, we can write the first equation as:
s+p=60
- Shirts are sold for $30 each and pants for $60 each.
- The total revenue from selling shirts and pants during the sale is $2,250.
- Thus, we can write the second equation as:
30s+60p=2250
1. Total items sold on a regular day:
- It is given that on a regular day, Bailey's sells 23 of the total items sold during the sale.
- Therefore, the total number of shirts and pants sold on a regular day is:
s+p=23×60=40
- We need to find the regular prices of shirts and pants.
- Since shirts are sold at a 20% discount for $30, the original price X of a shirt can be calculated as follows:
X−0.2X=30⟹0.8X=30⟹X=300.8=37.5
- Similarly, for pants sold at a 20% discount for $60:
Y−0.2Y=60⟹0.8Y=60⟹Y=600.8=75
- Therefore, the revenue equation for a regular day, where s shirts and p pants are sold, is:
37.5s+75p=1875
Now we have the following system of equations for a regular day:
1. s+p=40
2. 37.5s+75p=1875
The correct system of equations that yields the number of shirts s and the number of pants p sold during a regular day is:
1. s+p=40
2. 37.5s+75p=1875
Topper's Solved these Questions
Similar Questions
Read the following graph and answer the following question.
Find the ratio of the number of shirts of size 38 sold to the number of shirts of size 42 sold.
 View Solution
View SolutionSuppose you have 5 shirts , 4 pairs of pants , and 9 ties .How many outfits can be made consisting of a shirt , a pair of pants , and a tie ?
View Solution
Knowledge Check
- Question 1 - Select One
Tickets for a concert cost $4.50 for children and $12.00 for adults. 4460 concert tickets were sold for a total cost of $29,220. Solving which of the following systems of equations yeilds the number of children, c, and numbr of adults, a, that purchased concert tickets?
Ac+a=4460
4.50+12a=58.440Bc+a=4460
4.50c+12a=29,220Cc+a=4460
4.50c+12a=14,610Dc+a=29,220
4.50c+12a=4460 - Question 2 - Select One
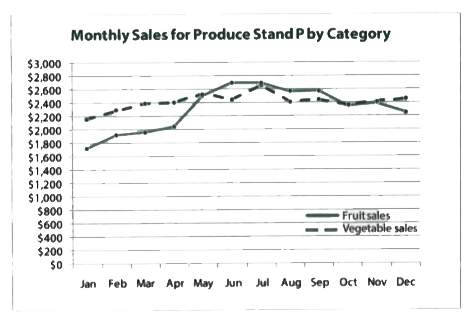
Over which of the following sequences of months did total sales decline the most?AFeb - MarBMar - AprCJun - JulDAug - Sep - Question 3 - Select One
A store sells shirts fro $7.50 each and hats for $5.00 each. The store earns $1,822.50 in one day from selling a total of 307 shirts and hats. How many shirts were sold on that day?
A37B89C115D202
The marked price of shirt was Rs 165 and it was sold at a discount of 12%. Find the discount allowed on the shirt and also its selling price.
View SolutionTwo types of tickets were sold for a concert held at an amphitheater. Tickets to sit on a bench during the concert cost $75 each, and tickets to sit on the lawn during the concert cost $40 each. Organizers of the concert announced that 350 tickets had been sold and that $19,250 had been raised through ticket sales alone. Which of the following systems of equations could be used to find the number of tickets for bench seats, B, and the number of tickets for lawn seats, L, that were sold for the concert?
View SolutionHannah placed an online order for shirts that cost $24.50 per shirt. A tax of 7% is added to the cost of the shirts, before a flat, untaxed shipping rate of $6 is charged. Which of the following represents Hannah's total cost for s shirts, in dollars?
View SolutionThe original price of a shirt is x dollars. During a sale , the original price is marked down y percent. On the last day of the sale , an additional discount of z percent off the sale price is offered. Which of the following represents the price of the shirt , in dollars , after the additional discount ?
View SolutionA student has 8 shirts , 5 pairs of pants , and 3 pairs of shoes , how many outfits consisting of a shirt , pair of pants , and pair of shores can this student form ?
View Solution

