AR3−Ar3+AR2h−Ar2hSolution in Bengali
The correct Answer is:A(R−r)(R2+Rr+r2+hR−hr)
Step by step video, text & image solution for AR^(3)-Ar^(3)+AR^(2)h-Ar^(2)h by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FACTORISATIONBOOK - CALCUTTA BOOK HOUSECHAPTER - FACTORISATIONEXERCISE - EXERCISE 2.2 (C Factorise the following polynomials )
18 Videos
- FACTORISATIONBOOK - CALCUTTA BOOK HOUSECHAPTER - FACTORISATIONEXERCISE - EXERCISE 2.2 (D Calculate)
7 Videos
- FACTORISATIONBOOK - CALCUTTA BOOK HOUSECHAPTER - FACTORISATIONEXERCISE - EXERCISE 2.2 (A Factorise the following polynomials )
5 Videos
- DISTANCE FORMULAS BOOK - CALCUTTA BOOK HOUSECHAPTER - DISTANCE FORMULAS EXERCISE - Long answer
11 Videos
- FREQUENCY DISTRIBUTIONS OF GROUPED DATA BOOK - CALCUTTA BOOK HOUSECHAPTER - FREQUENCY DISTRIBUTIONS OF GROUPED DATA EXERCISE - EXERCISE-1 (LONG TYPE ANSWER QUESTION)
14 Videos
Similar Questions
8a3−27b3−1−18ab
View Solution(101)3−(51)3−(50)3
View Solutionx3−19x−30
View SolutionIf the distance between the points (7,3) and (2,y) be √41 units. Find y .
View SolutionDefine:
class-interval
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
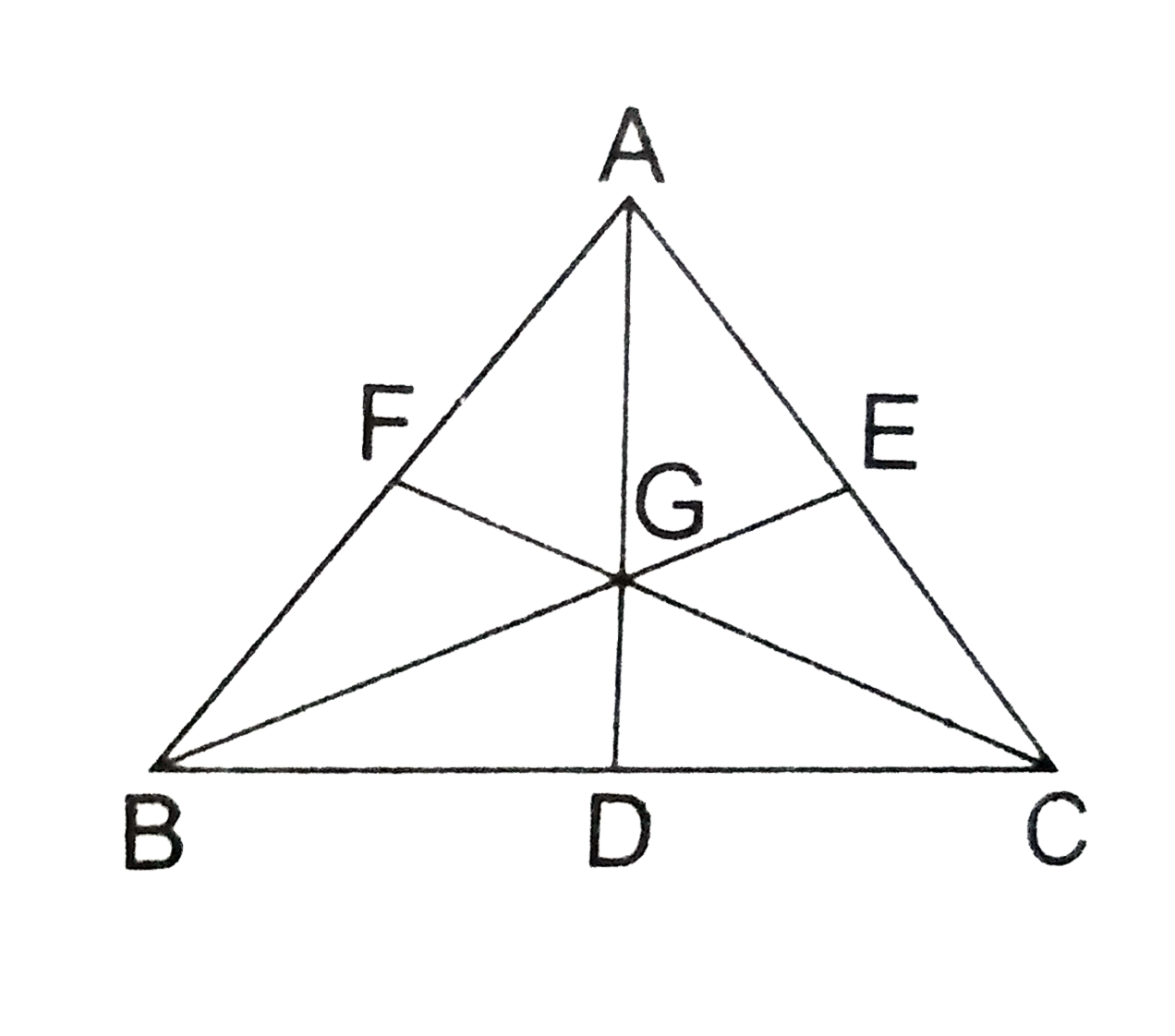
View Solutionयदि ΔABC की माध्यिकायें बिंदु G पर प्रतिच्छेद करती है, तो सिद्ध कीजिए कि
ar(ΔAGB)=ar(ΔAGC)=ar(ΔBGC)=13ar(ΔABC)
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View Solutionत्रिभुज ABC की AD एक माध्यिका है तथा भुजा AC पर बिंदु P इस प्रकार है कि
ar(ΔADP):ar(ΔABD)=2:3, तो ar(ΔPDC):ar(ΔABC)
View SolutionHe, H , Ne , Ar
View SolutionIf a,ar,ar2,ar3,....... are in G.P,then the sum of infinite terms of GP, if |r|<1=
View SolutionIf s=a+ar+ar2+ar3+.......∞ then s∞=. (|r|<1)
View SolutionThe products of the corresponding terms of the sequences a,ar,ar2,…arn–1 and A,AR,AR2,…ARn–1 form a
View SolutionIf the median of a △ABC intersect at G. show that ar (△AGC) = ar (△AGB) = ar (△BGC) = 1/3 ar (△ABC)
View SolutionIf the medians of a triangle ABC meet at G, prove that ar (AGB) = ar (AGC) = ar (BGC) = (1)/(3) is ar (ABC).
View Solution
