a+ar+ar2+...+∞=15
a2+(ar)2+(ar2)2+...+∞=150 .
Find ar2+ar4+ar6+...∞
12
25
16
None
The correct Answer is:A
To solve the problem, we start with the two given equations:
1. S1=a+ar+ar2+…=15
2. S2=a2+(ar)2+(ar2)2+…=150
Step 1: Express the sums in terms of a and r
The sum of an infinite geometric series can be expressed as:
S=a1−r
For the first equation:
a1−r=15(1)
For the second equation, we note that:
S2=a2+(ar)2+(ar2)2+…=a21−r2
Thus, we have:
a21−r2=150(2)
Step 2: Solve for a and r
From equation (1), we can express a in terms of r:
a=15(1−r)(3)
Substituting equation (3) into equation (2):
(15(1−r))21−r2=150
Expanding this gives:
225(1−r)21−r2=150
Cross-multiplying yields:
225(1−r)2=150(1−r2)
Expanding both sides:
225(1−2r+r2)=150(1−r2)
This simplifies to:
225−450r+225r2=150−150r2
Combining like terms:
375r2−450r+75=0
Step 3: Simplify the quadratic equation
Dividing the entire equation by 75:
5r2−6r+1=0
Step 4: Use the quadratic formula to find r
Using the quadratic formula r=−b±√b2−4ac2a:
r=6±√(−6)2−4⋅5⋅12⋅5
Calculating the discriminant:
r=6±√36−2010=6±√1610=6±410
Thus, we have two potential solutions for r:
r=1010=1(not valid for a converging series)
r=210=15
Step 5: Find a
Substituting r=15 back into equation (3):
a=15(1−15)=15⋅45=12
Step 6: Find ar2+ar4+ar6+…
This series can be expressed as:
ar2+ar4+ar6+…=ar2(1+r2+r4+…)
The sum of the infinite series 1+r2+r4+… is:
11−r2
Thus, we have:
ar2⋅11−r2
Calculating ar2:
ar2=12⋅(15)2=12⋅125=1225
Now substituting r2=(15)2=125:
1−r2=1−125=2425
Thus, the sum becomes:
12252425=1224=12
Final Answer
The value of ar2+ar4+ar6+… is:
12
2. S2=a2+(ar)2+(ar2)2+…=150
r=210=15
Similar Questions
Knowledge Check
Let sum of ten numbers a,ar,ar2,...Ar9 is 18 and sum of their reciprocal is 6 then product of these ten numbers is.
A324B343C243D724In the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
 A14cm2B7cm2C21cm2D28cm2
A14cm2B7cm2C21cm2D28cm2In figure, if ar(ΔABC) = 28 cm2, then find ar( IIgm AEDF).
 A21 cm2B18 cm2C16 cm2D14 cm2
A21 cm2B18 cm2C16 cm2D14 cm2
Let a+ar1+ar12++∞anda+ar2+ar22++∞ be two infinite series of positive numbers with the same first term. The sum of the first series is r1 and the sum of the second series r2. Then the value of (r1+r2) is ________.
View SolutionShow that the products of the corresponding terms of the sequences a, ar,ar2,.......,arn−1and A,AR,AR2,......,ARn−1,form a G.P, and find the common ratio.
View SolutionIn the given figure, DE || BC, DE= 3 cm, BC = 9 cm and ar (DADE) = 30cm2. Find ar (BCED).
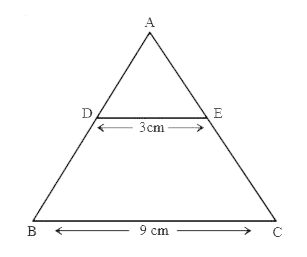
View SolutionShow that the products of the corresponding terms of the sequences a,ar,ar2,...,arn−1anda,AR,AR2,....,ARn−1 form a G.P., and find the common ratio.
View SolutionIn ΔABC~ΔDEFandar(ΔABC)=100cm2,ar(ΔDEF)=196cm2andDE=7cm, then find AB.
View Solution

