A particle is moving on a circular path under the action of only one force action always toward the fixed point on the circumference. Find the ratio of &
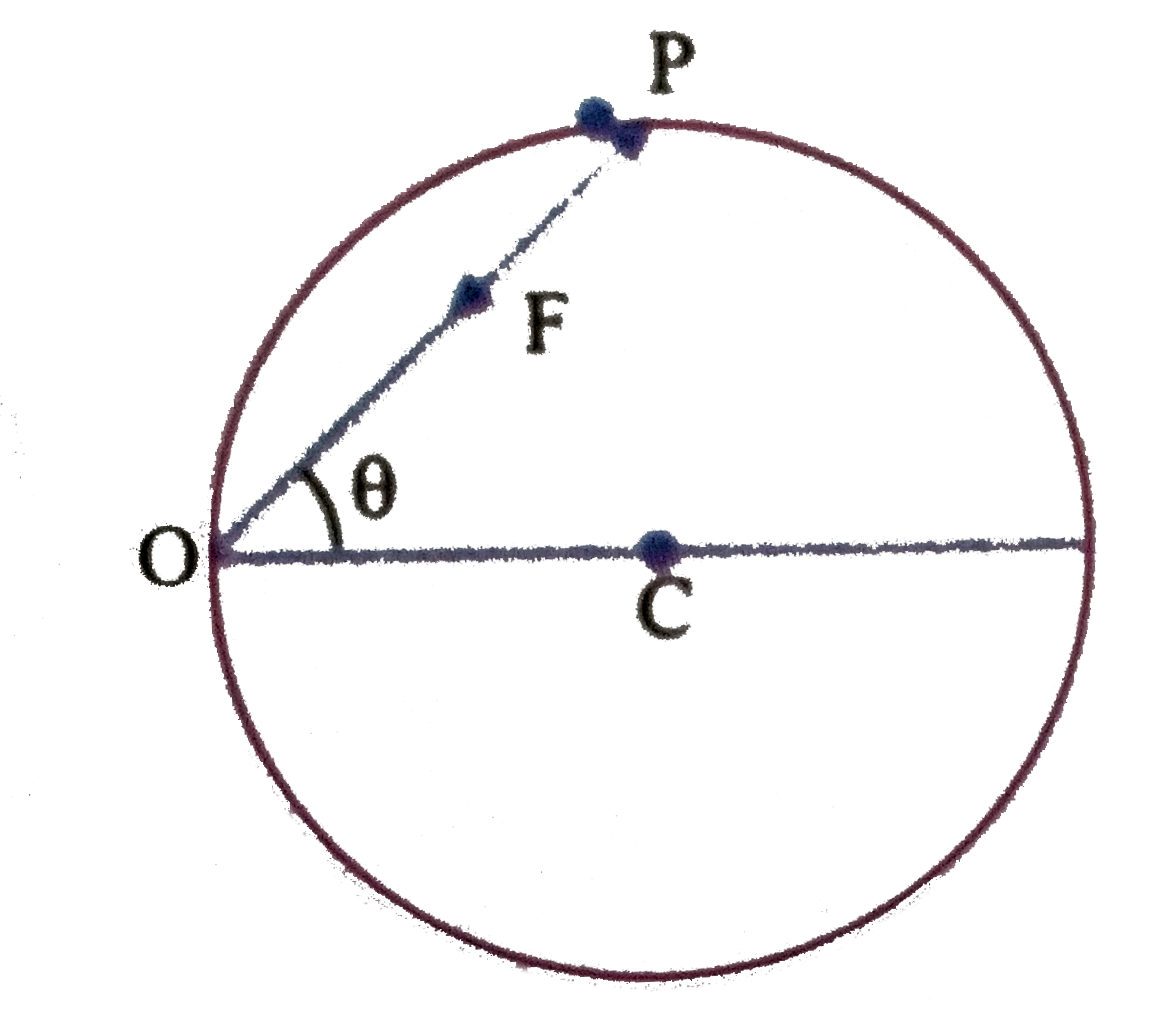
2 tan
tan
The correct Answer is:A

F cos
Angular velocity '' of line joining 'P' and 'C' is
Tangential acceleration of particle about 'd' ,
But
, Hence
On solving ,
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - More than one correct18videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Assertion - Reason12videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice23videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston14videos
MOTION IN A STRAIGHT LINE
Similar Questions
A charged particle is moving in a circular path under the action of the Lorentz force. How much work is done by the force in one revolution?
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
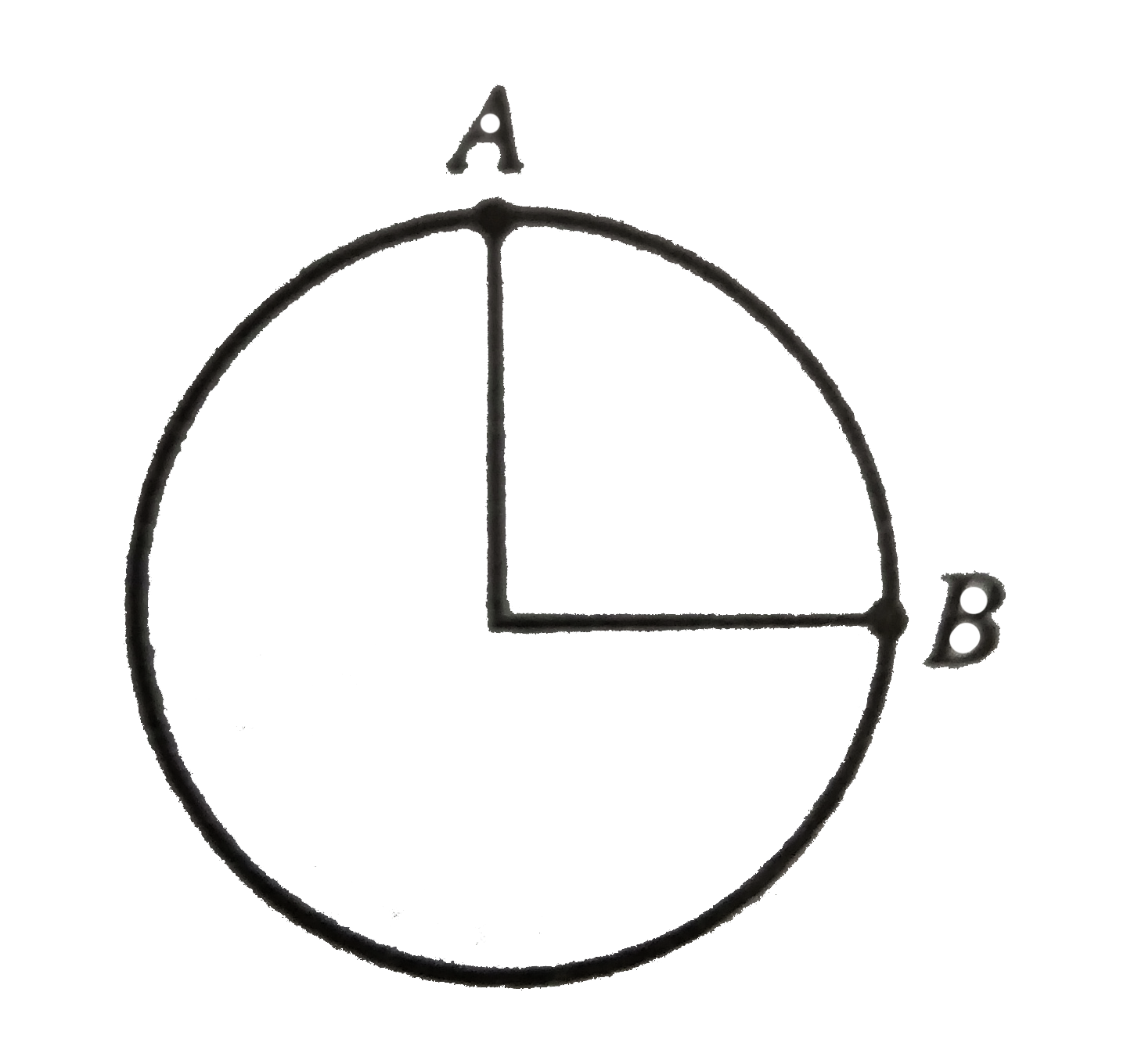 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle 'P' is moving on a circular under the action of only one force action always toward the fixed point 'O' on the circumference. Find the ratio of d2θdt2 & (dθdt)2
 A2tanθBtanθCtanθ2Dtanθ3
A2tanθBtanθCtanθ2Dtanθ3 - Question 2 - Select One
A particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
A−32ka2B−k4a2Ck2a2DZero - Question 3 - Select One
A particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
A→F.→v=0B→F.→c>0C→F.→v<0D→F.→v≥0
Charged particle of charge q mass m moves in a circular path of radius r under the action of force F .The equivalent current is
View SolutionCharged particle of charge q mass m moves in a circular path of radius r under the action of force F .The equivalent current is
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA particle of mass 'm' moves with a constant speed along a circular path of radius r under the action of a force F .Its speed is given by
View Solution

