In Q.48 , the block can be made to slide on the floor only if θ is more than a minimum value . Otherwise , the block cannot be made to slide by any value of F however large . Minimum value of θ for less than which sliding cannot happen , is :
sin−1(μ√1+μ2)
cos−1(μ√1+μ2)
tan−1(μ√1+μ2)
zero
The correct Answer is:A
See Q.48. For motion , F must be positive .
∴ sin θ−μcos θ>0
sin θ>μcosθ
tanθ>μ
From the figure ,
sinθ>μ√1+μ2
θ>sin−1(μ√1+μ2)

Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - More than one correct18videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Assertion - Reason12videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice23videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston14videos
MOTION IN A STRAIGHT LINE
Similar Questions
The handle of a floor mop makes an angle θ with the vertical. If μkandμs be the coefficients of kinetic and static friction between floor and mop, show that if θ is smaller than certain value θ0, the mop cannot be made to slide over across the floor, no matter how great a force is directed along the handle towards the centre. What is the angle θ0 ?
View SolutionA block placed on a horizontal surface is being pushed by a force F making an angle θ with the vertical as shown in Fig. 7.39 . The coefficient of friction between block and surface is μ . (a) Find the force required to slide the block with uniform velocity on the floor . (b) Show that if θ is smaller than a certain

angle θ0 , the block cannot be made to slide across the floor , no matter how great the force be .View Solution
Knowledge Check
- Question 1 - Select One
The minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
Ag(cosθ+μsinθsinθ−μcosθ)Bg(sinθ+μcosθcosθ−μsinθ)Cg(sinθ−μcosθsinθ+μcosθ)Dg(cosθ−μsinθsinθ+μcosθ) - Question 2 - Select One
If the friction is sufficient to prevent the block from sliding, then the minimum value of F for which the cube begins to topple about an edge is
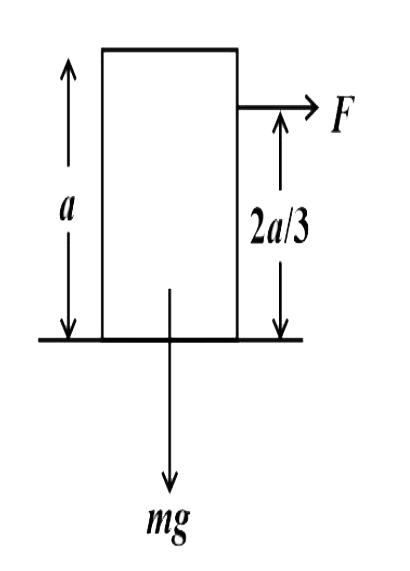 A23mgB34mgC12mgDmg
A23mgB34mgC12mgDmg - Question 3 - Select One
The arrangement is released from rest. The minimum angle θ at which block A starts sliding downwards is
 Atanθ=0Btanθ=0.5Ctanθ=16Dtanθ=13
Atanθ=0Btanθ=0.5Ctanθ=16Dtanθ=13
A block is rotating in contact with vertical wall (rotor) as shown. Find the minimum value of ω so that the block does not slide down.
 View Solution
View SolutionA solid cube of side 'a' is shown in the figure. Find maximum value of 100ba for which the block does not topple before sliding.
 View Solution
View SolutionInitially the system is at rest. find out minimum value of F for which sliding starts between the two blocks.
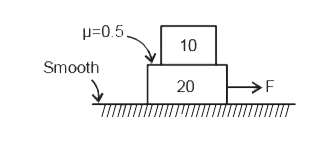 View Solution
View SolutionShow that the maximum value of f(x)=x+1x is less than its minimum value.
View SolutionA block of mass m is placed at rest on a horizontal rought surface with angle of friction ϕ. The block is pulley with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View Solution

