A 20kg block is originally at rest on a horizontal surface for which the coefficient of friction is 0.6. A horizontal force F is applied such that it varies with time as shown in the figure (a) & (b). If the speed of the block after 10s is 8v then find v. ( Take g=10m/s2)
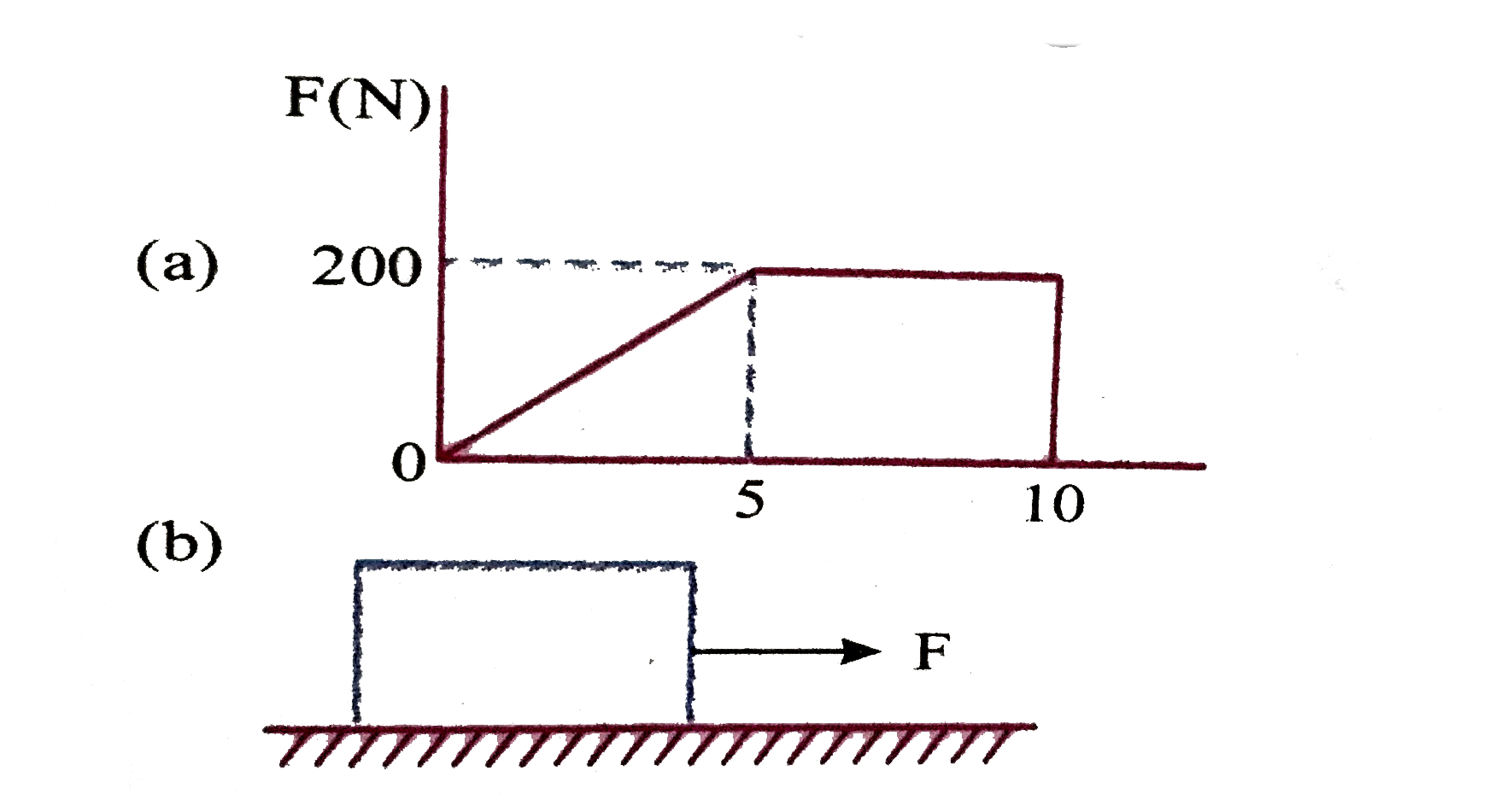
The correct Answer is:3
F−μmg=mdvdt
m∫v0dv=∫103dt−μmg∫103dt
⇒20v=480⇒v=24
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Matrix - Match
5 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
A 20 kg block is originally at rest on a horizontal surface for which the coefficient of friction is 0.6 . A horizontal force F is applied such that it varies with time as shown in the figure (a) and (b) . If the speed of the block after 10 s is 8 v then find v . (Take g = 10m/s2)

View SolutionA block of mass 1 kg start moving at t = 0 with speed 2m/s on rough horizontal surface with coefficient of friction 0.2. A horizontal force F is applied in the direction of velocity which varies with time as shown in figure. Find the speed (in m/s) of particle at t = 3 s.

View Solution
Knowledge Check
A block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .
 A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2
A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2A 10 kg block is placed on a horizontal surface whose coefficient of friction is 0.2.A horizontal force P = 15 N first acts on it in the eastward direction. Later, in addition to P a second horizontal force Q = 20 N acts on it in the northward direction: (Take g=10ms2)
AThe block will not move when only P acts, but will move when both P and Q act.BIf the block moves,the acceleration will be 0.5ms2.CWhen the block moves, its direction of motion will be tan−1(34) east of northDWhen both P and Q act, the direction of the force of friction acting on the block will be tan−1(34) west of southA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθ
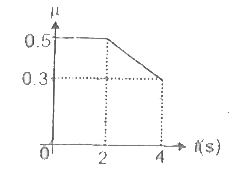
A block is projected with speed 20 m/s on a rough horizontal surface. The coefficient of friction (μ) between the surface varies with time (t) as shown in figure. The speed of body at the end of 4 second will be (g=10m/s2)
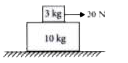
View SolutionA 3kg block is placed over a 10kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.2. IF a horizontal force of 20N is applied to 3kg block. Find the acceleration of the two blocks.
View SolutionA block of mass 1kg is at rest on a rough horizontal surface having coefficient of static friction 0.2 and kinetic friciton 0.15, find the frictional forces if a horizontal force,
(a) F=1N (b) F=1.96N (c) F=2.5N is applied on a block

View Solution2gk block is kept on 1kg block as shown . The friction between 1kg block and fixed surface is absent and the coefficient of friction between 2kg block is μ=0.1. A constant horizontal force F=4N is applied on 1kg block. If the work done by the friction on 1kg block in 2s is −XJ, then find X. Take g=10m/s2.

View SolutionA horizontal force of 1.2kg is applied on a 1.5kg block, which rests on a horizontal surface If the coefficient of friction is 0.3 find the acceleration produced in the block.
View Solution
