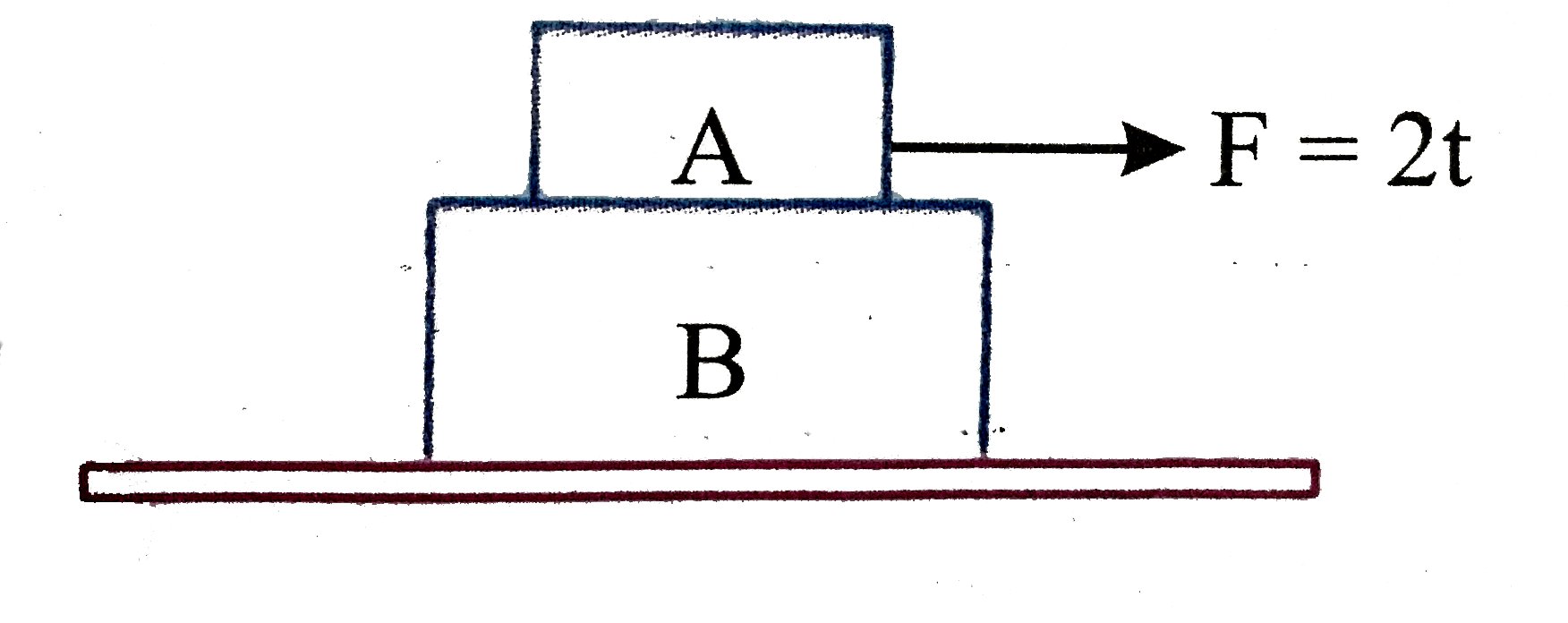
Two blocks A and B of mass 2kg and 4kg are placed one over the others as shown in figure. A time vaying horizontal force F=2t is applied on the upper blocks as shown in figure. Here t is in second and F is in newton. Coefficient of friction between A and B is μ=12 and the horizontal surface over which B is placed is smmoth. (g=10m/s2). If acceleration of blocks A as a function of time is given by aA=t/c then find value of c. (t≤7.5s)
The correct Answer is:3
As aA=(tc)

Limiting friction between A and B is
fL=μMAg=10N

Block B moves due to friction only
∴ Maximum acceleration of B
amax=fLMB=2.5m/sec2
2.5=F(mA+mB)=2t6
∴ t=7.5 seconds .
Hence , for t≤7.5 seconds .
aA=aB=t3
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Matrix - Match5videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston14videos
MOTION IN A STRAIGHT LINE
Similar Questions
Two blocks A and B of masses 2kg and 4kg are placed one over the other as shown in figure. Atime varying horizontal force F=2t is applied on the upper block as shown in figure. Here t is in second and F is in newton. Drow a graph showing acceleration of A and B on y-axis and time on x-axis.Coefficient of friction between A and B is μ=12 and the horizontal surface over which B is placed smooth. (g=10m/s2)
 View Solution
View SolutionTwo blocks A and B of mass 2 kg and 4 kg are placed one over the other as shown in Fig. (a) . A time varying horizontal force F = 2t is applied on the upper block . Here t is in second and F is in newton . A graph drawn between accelerations of A and B on y-axis and time on x-axis is shown in Fig. (b) . Then tan θ=1K , K = .....
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied on a 1-kg block. Find the force of interaction of the blocks.

A4NB5NC10NDnone - Question 2 - Select One
Two block A and B of mass 50kg and 300kg respectively are placed as shown in figure. Coefficient of friction between all surface is 12
Then (take g=10m/s)
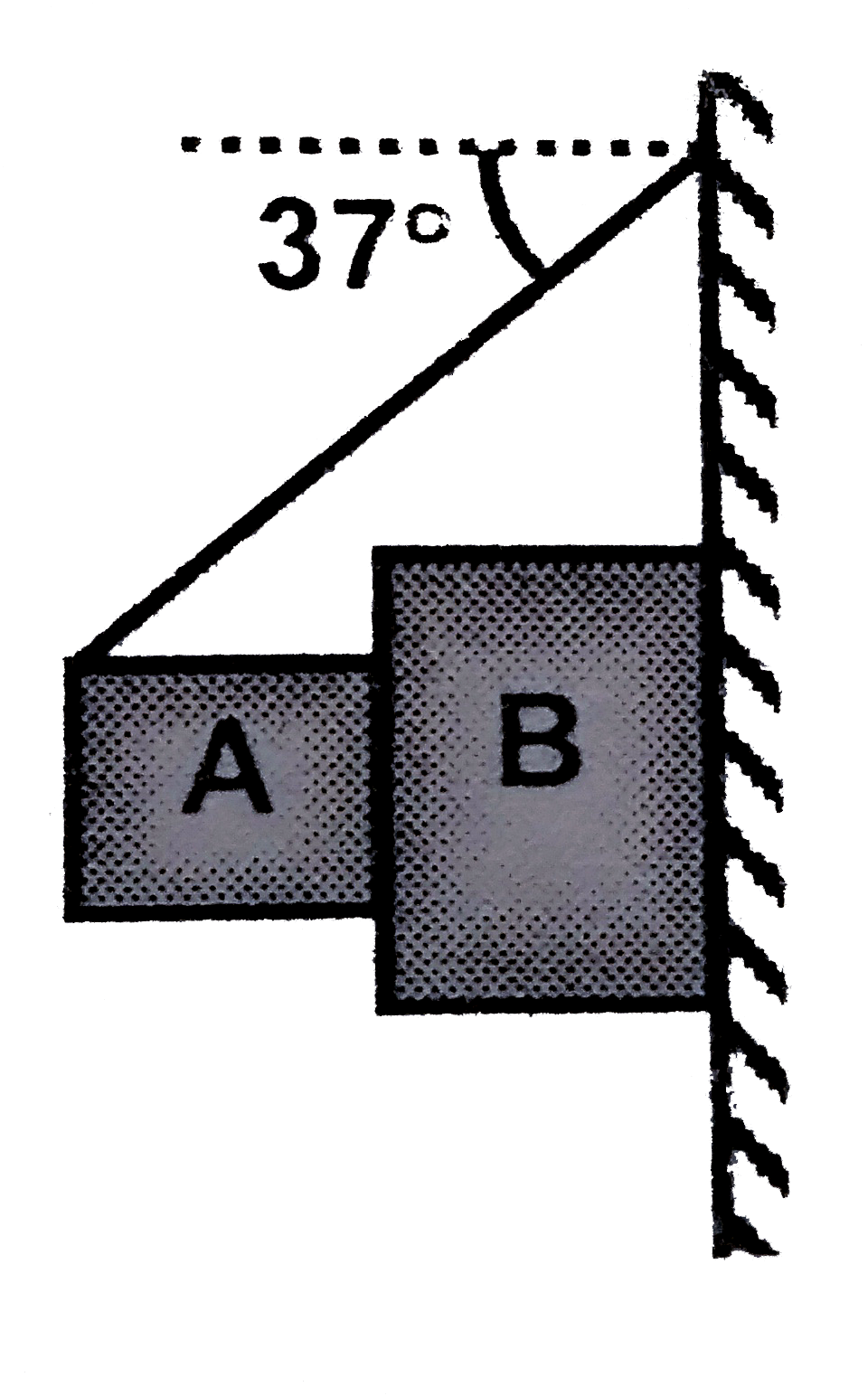 ATension in the string is 2000NBTension in the string is 3000NCAcceleration of block B is 5/3m/s2DAcceleration of block B is 10/3m/s2
ATension in the string is 2000NBTension in the string is 3000NCAcceleration of block B is 5/3m/s2DAcceleration of block B is 10/3m/s2 - Question 3 - Select One
Two blocks of masses m and 2 m are placed one over the other as shown in figure.The coefficient of friction between m and 2m is μ and between 2m and ground is μ3. If a horizontal force F is applied on upper block and T is tension developed in string, then choose the incorrect alternative.
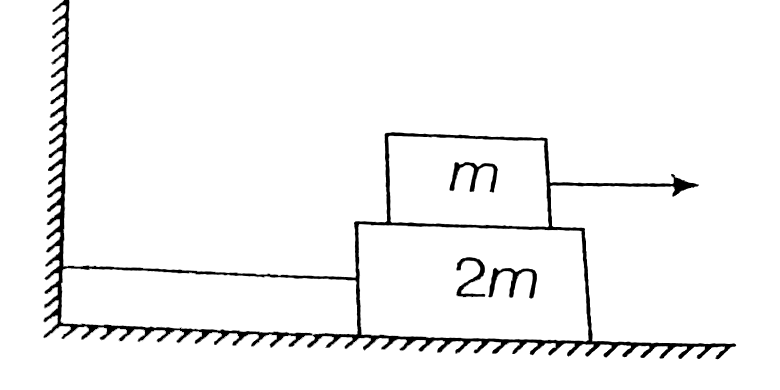 AIf F=μ3mg, T=0BIf F=μmg, T=0CIf F=2μmg,T=μmg3DIf F=3μmg,T=0
AIf F=μ3mg, T=0BIf F=μmg, T=0CIf F=2μmg,T=μmg3DIf F=3μmg,T=0
Two blocks of masses 4kg and 2kg are placed side on a smooth horizontal surface as shown in the figure. A horizontal force of 20N is applied on 4kgblock. Find
(a) the acceleration of each block.
(b) the normal reaction between two blocks.
 View Solution
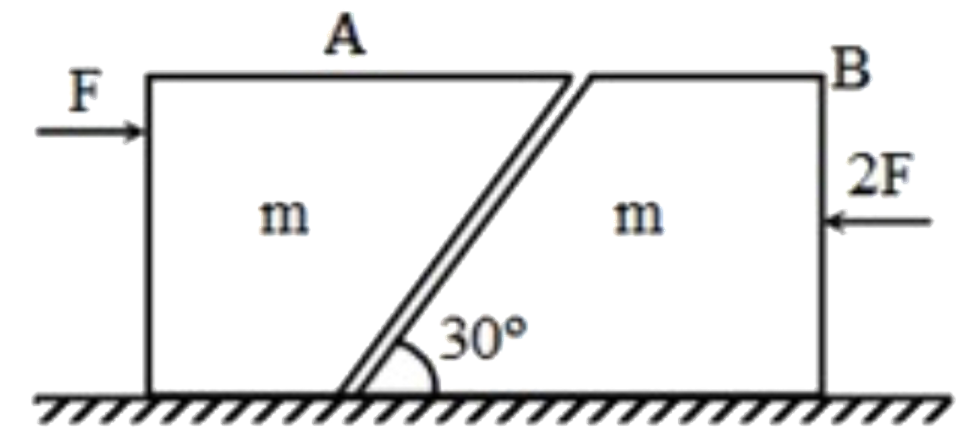
View SolutionTwo blocks 'A' and 'B' each of mass 'm' are placed on a smooth horizontal surface . Two horizontal force F and 2F are applied on the blocks A and B , respectively , as shown in figure . The block A does not slide on block B . The normal reaction acting between the two blocks is
 View Solution
View SolutionTwo blocks A and B of mass 10 kg and 20 kg respectively are placed as shown in figure .Coefficient of friction between all the surface is 0.2 (g=10m/s2) Then,
 View Solution
View SolutionTwo blocks of equal mass 2 kg are placed on a rough horizontally surfaces as shown and a force F is applied on the upper block . The system is initially at rest . Find acceleration of the lower block in m/s2 .
 View Solution
View SolutionTwo blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 View Solution
View Solution

