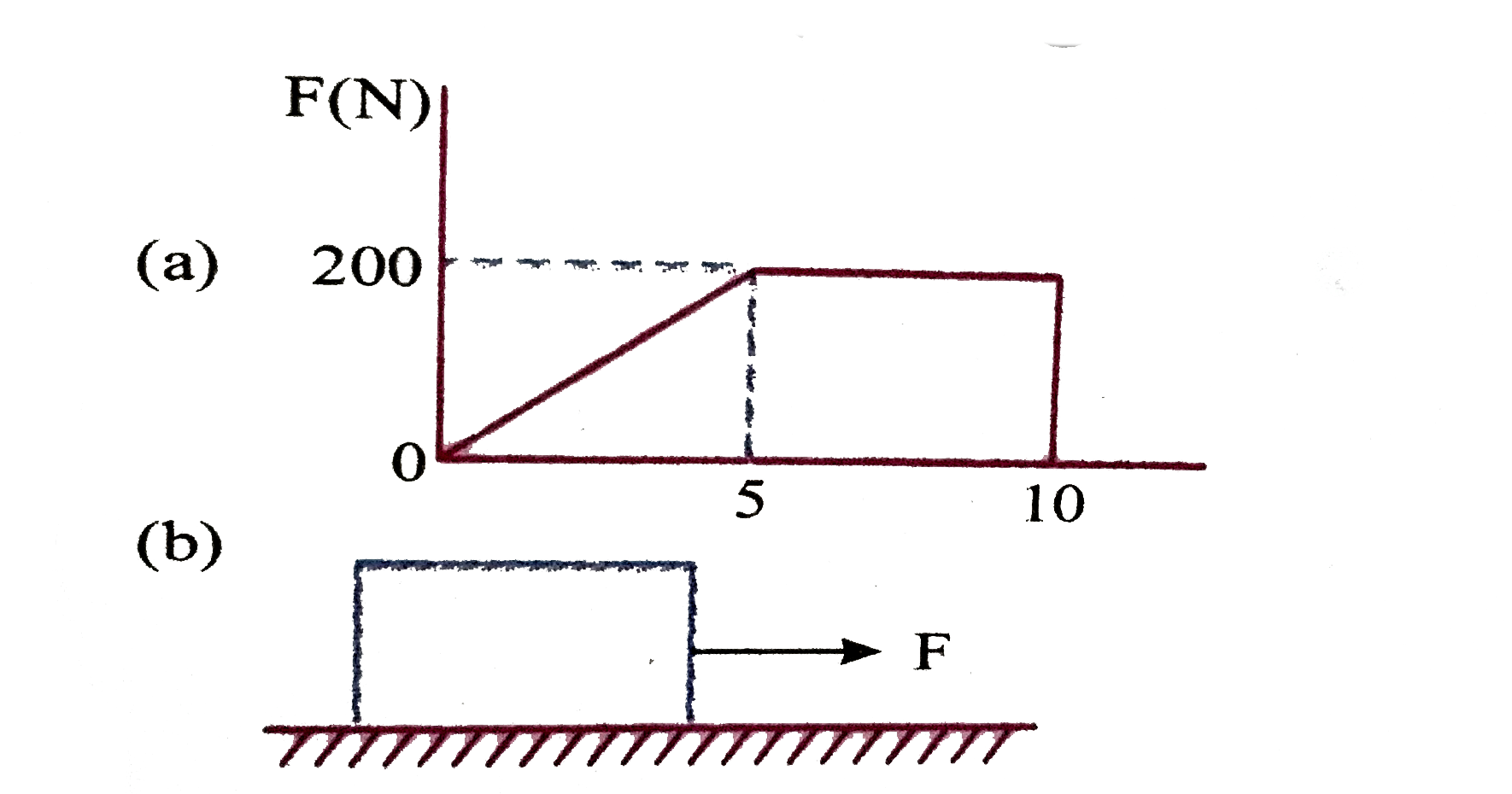
A 20 kg block is originally at rest on a horizontal surface for which the coefficient of friction is 0.6 . A horizontal force F is applied such that it varies with time as shown in the figure (a) and (b) . If the speed of the block after 10 s is 8 v then find v . (Take g = 10m/s2)

The correct Answer is:3
flimit=0.6N = 0.6 mg = 0.6×20×10=120N
The equation for the applied force is
F = 40 t = 200 , for t≤5, 5≤t≤10
The limiting friction acts as t≥3 second.
Using impulse equation ,
t∫0Fdt=(pf−pi)
5∫3(40t−120)dt+10∫5(200−120)dt=20v1
402(25−9)−120(2)+80×(10−5)=20v1
320−240+400=20v1
∴ v1=24=8v
∴ v=3
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Matrix - Match
5 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
A 20kg block is originally at rest on a horizontal surface for which the coefficient of friction is 0.6. A horizontal force F is applied such that it varies with time as shown in the figure (a) & (b). If the speed of the block after 10s is 8v then find v. ( Take g=10m/s2)
View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View Solution
Knowledge Check
A block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .
 A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2
A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2A rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30∘ with the horizontal plane , what is the force of friction on the block ? (Take g = 10m/s2)
A5 NB10 NC12 ND20 N
A block of mass 1 kg start moving at t = 0 with speed 2m/s on rough horizontal surface with coefficient of friction 0.2. A horizontal force F is applied in the direction of velocity which varies with time as shown in figure. Find the speed (in m/s) of particle at t = 3 s.
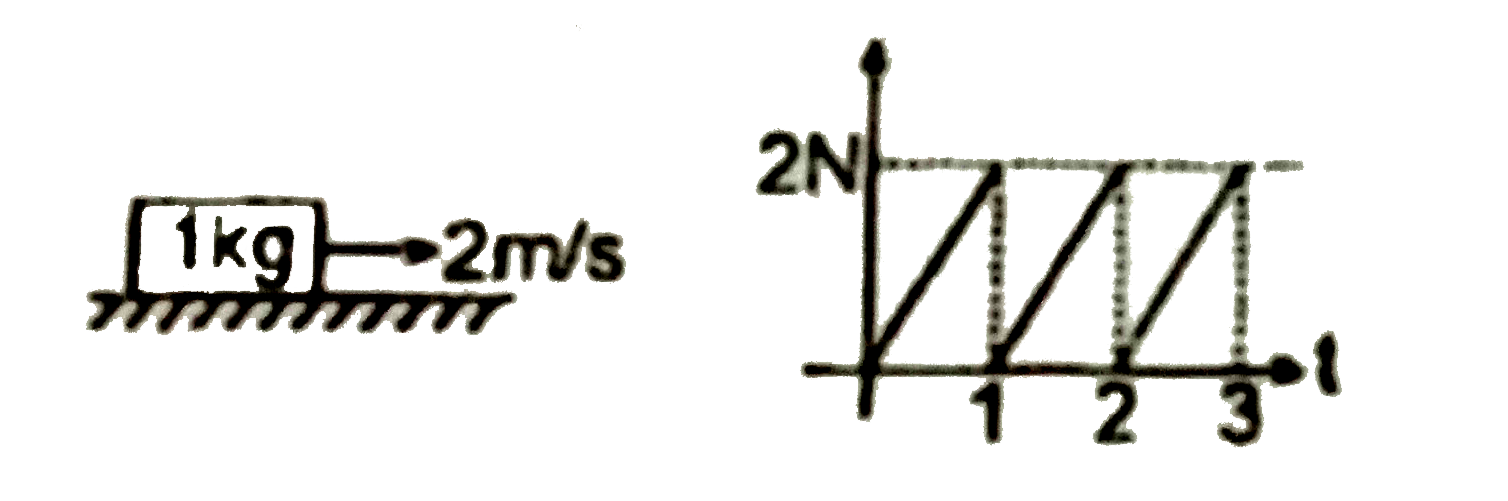
View Solution2gk block is kept on 1kg block as shown . The friction between 1kg block and fixed surface is absent and the coefficient of friction between 2kg block is μ=0.1. A constant horizontal force F=4N is applied on 1kg block. If the work done by the friction on 1kg block in 2s is −XJ, then find X. Take g=10m/s2.
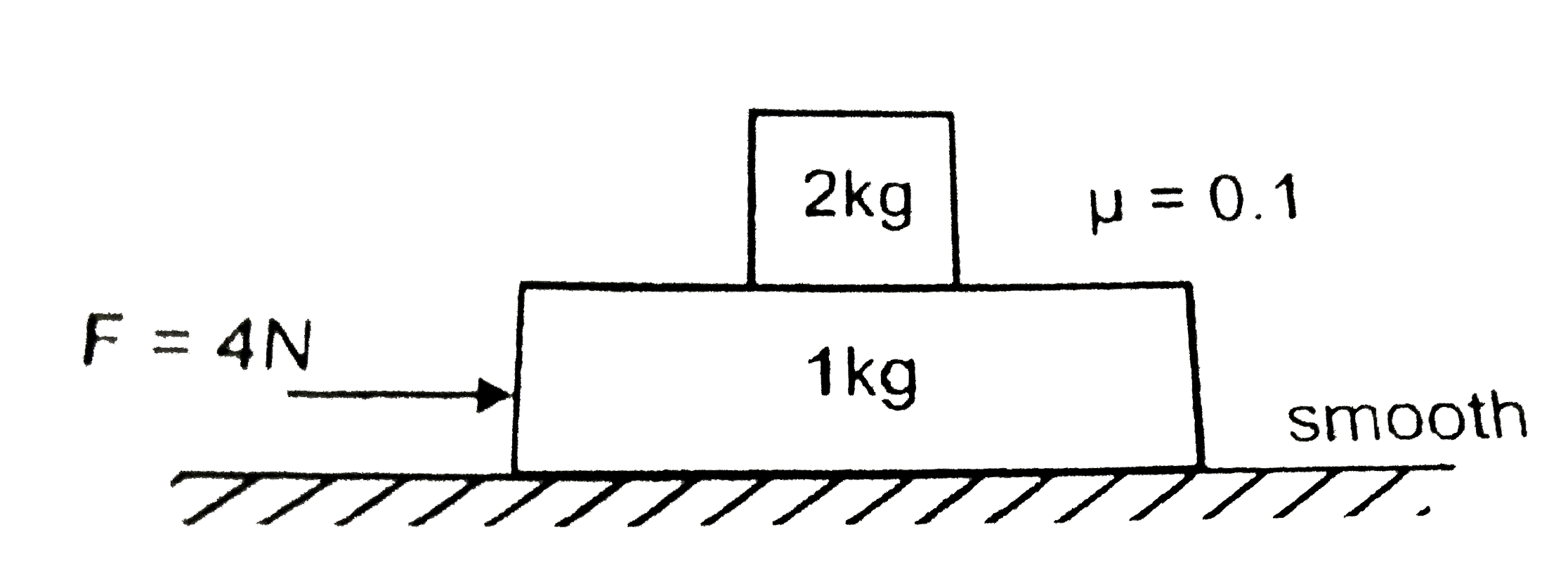
View Solution2gk block is kept on 1kg block as shown . The friction between 1kg block and fixed surface is absent and the coefficient of friction between 2kg block is μ=0.1. A constant horizontal force F=4N is applied on 1kg block. If the work done by the friction on 1kg block in 2s is −XJ, then find X. Take g=10m/s2.

View SolutionA horizontal force of 1.2kg is applied on a 1.5kg block, which rests on a horizontal surface If the coefficient of friction is 0.3 find the acceleration produced in the block.
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View Solution
